
分析 设鸡场的宽为xm,则长可用含x的代数式表示,从而这个鸡场的面积可用含x的代数式表示,列方程求解,然后对a进行讨论确定答案.
解答 解:设养鸡场垂直于墙的一边长为xm,则平行于墙的边长为(40-2x)m,由题意得.
x(40-2x)=150,
整理,得x2-20x+75=0,
解方程,得x1=15,x2=5.
当x=15时,40-2x=10;
当x=5时,40-2x=30.
答:当a<10时,问题无解;
当10≤a<30时,问题有一解,即宽为10m,长为15m;
当a≥30时,问题有两解,可建宽为10m,长为15m或宽为5m,长为30m的鸡场.
点评 本题考查的是一元二次方程的应用.注意解题时需要从实际出发,知道a对鸡场长度起到限制作用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
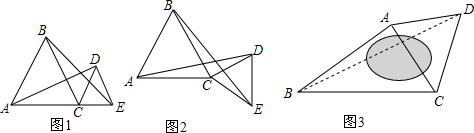
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
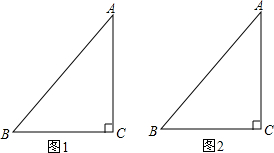 已知△ABC,∠C=90°,AC=4,BC=3.
已知△ABC,∠C=90°,AC=4,BC=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
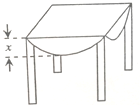 用一块直径为4米的圆桌布平铺在对角线长为4米的正方形桌面上(如示意图),若四周下垂的最大长度相等,则这个最大长度x为0.6米($\sqrt{2}$取1.4).
用一块直径为4米的圆桌布平铺在对角线长为4米的正方形桌面上(如示意图),若四周下垂的最大长度相等,则这个最大长度x为0.6米($\sqrt{2}$取1.4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
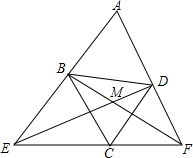 如图,菱形ABCD中∠A=60°,过点C的直线分别交AB、AD的延长线于E、F,BF与DE相交于M.求证:
如图,菱形ABCD中∠A=60°,过点C的直线分别交AB、AD的延长线于E、F,BF与DE相交于M.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com