
【题目】计算
(1)(+3.5)﹣1.4﹣(2.5)+(﹣4.6)
(2)[2﹣5×(﹣ ![]() ) 2]÷(﹣
) 2]÷(﹣ ![]() )
)
(3)[2 ![]() ﹣(
﹣( ![]() +
+ ![]() ﹣
﹣ ![]() )×24]÷5×(﹣1)2009
)×24]÷5×(﹣1)2009
(4)﹣22+|5﹣8|+24÷(﹣3)× ![]()
(5)(xy2﹣x2y)﹣2( xy+xy2)+3x2y
(6)5a2﹣[a2+(5a2﹣2a)﹣2(a2﹣3a)].
【答案】
(1)解:原式=3.5﹣1.4﹣2.5﹣4.6
=﹣5.
(2)解:原式=[2﹣5× ![]() ]×(﹣4)
]×(﹣4)
= ![]() ×(﹣4)
×(﹣4)
=﹣3.
(3)解:原式=[ ![]() ﹣(﹣
﹣(﹣ ![]() )×24]÷5×(﹣1)
)×24]÷5×(﹣1)
= ![]() ÷5×(﹣1)
÷5×(﹣1)
=﹣ ![]() .
.
(4)解:原式=﹣4+3﹣8× ![]()
=﹣1﹣ ![]()
=﹣ ![]()
(5)解:原式=xy2﹣x2y﹣2 xy﹣2xy2+3x2y
=﹣xy2+2x2y﹣2xy
(6)解:原式=5a2﹣[a2+5a2﹣2a﹣2a2+6a]
=5a2﹣[4a2+4a]
=a2﹣4a
【解析】结合整式加减法的运算法则进行求解即可.
【考点精析】关于本题考查的有理数的四则混合运算和整式加减法则,需要了解在没有括号的不同级运算中,先算乘方再算乘除,最后算加减;整式的运算法则:(1)去括号;(2)合并同类项才能得出正确答案.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】某人去水果批发市场采购苹果,他看中了A、B两家苹果.这两家苹果品质都一样,零售价都为6元/千克,但批发价各不相同. A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.
B家的规定如表:
数量范围(千克) | 0~500 | 500以上~1500 | 1500以上~2500 | 2500以上 |
价 格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
【表格说明:批发价格分段计算,如:某人批发苹果2100千克,则总费用=6×95%×500+6×85%×1000+6×75%×(2100﹣1500)】
根据上述信息,请解答下列问题:
(1)如果他批发1000千克苹果,则他在A 家批发需要元,在B家批发需要元;
(2)如果他批发x千克苹果(1500<x<2000),则他在A 家批发需要元,在B家批发需要元(用含x的代数式表示);
(3)现在他要批发不超过1000千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,D、E、F分别是射线BA、CB、AC上一点,且AD=BE=CF,连接DE、EF、DF.
(1)求证:∠BDE=∠CEF;
(2)试判断△DEF的形状,并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
每年6月5日是世界环境日,中国每年都有鲜明的主题,旨在释放和传递:建设美丽中国,人人共享,人人有责的信息,小明积极学习与宣传,并从四个方面A—空气污染,B—淡水资源危机,C—土地荒漠化,D—全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是他收集数据后,绘制的不完整的统计图表:

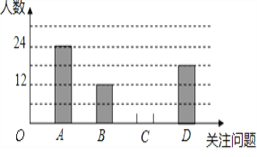
根据表中提供的信息解答以下问题:
(1)表中的![]() ________,
________, ![]() _________;
_________;
(2)请将条形统计图补充完整;
(3)如果小明所在的学校有4200名学生,那么根据小明提供的信息估计该校关注“全球变暖”的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一块均匀的不等边三角形的铁板,它的重心在( )
A. 三角形的三条角平分线的交点 B. 三角形的三条高线的交点
C. 三角形的三条中线的交点 D. 三角形的三条边的垂直平分线的交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=BC,AB=4,∠ACB=90°,以AB的中点D为圆心DC长为半径作![]() 圆DEF,设∠BDF=α(0°<α<90°),当α变化时图中阴影部分的面积为 (
圆DEF,设∠BDF=α(0°<α<90°),当α变化时图中阴影部分的面积为 (![]() 圆:∠EDF=90°,
圆:∠EDF=90°,![]() 圆的面积=
圆的面积=![]()
![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列性质中,等腰三角形具有而直角三角形不一定具有的是( )
A.任意两边之和大于第三边
B.有一个角的平分线垂直于这个角的对边
C.至少有两个角是锐角
D.内角和等于180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽暑假期间参加社会实践活动,从某批发市场以批发价每个m元的价格购进100个手机充电宝,然后每个加价n元到市场出售.
(1)求售出100个手机充电宝的总售价为多少元(结果用含m,n的式子表示)?
(2)由于开学临近,小丽在成功售出60个充电宝后,决定将剩余充电宝按售价8折出售,并很快全部售完. ①相比不采取降价销售,她将比实际销售多盈利多少元(结果用含m、n的式子表示)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com