练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    二次函数y=的图象如图，对称轴为．若关于的一元二次方程（为实数）在的范围内有解，则的取值范围是(    )

    A．    　　               B．

    C．  　　　                D．


    A


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，将三角板的直角顶点放在直尺的一边上，若∠1=65°，则∠2的度数为

    A. 10°.         B. 15°.    C. 20°.        D. 25°.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知等腰△ABC中，AD⊥BC于点D，且AD=BC，则△ABC底角的度数为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若x3+x2+x=-1，则的值是（　　）

    　   A． 2           B． 0                 C． ﹣1              D． 1

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    ．阅读理解并填空：

    （1）为了求代数式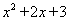的值，我们必须知道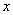的值．若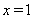，则这个代数式的值为_______；若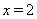，则这个代数式的值为_______，……，可见，这个代数式的值因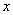的取值不同而_______（填“变化”或“不变”）．尽管如此，我们还是有办法来考虑这个代数式的值的范围．

    （2）把一个多项式进行部分因式分解可以来解决代数式值的最大（或最小）值问题．例如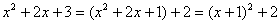：，因为是非负数，所以，这个代数式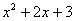的最小值是_______，这时相应的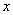的值是__________．

    尝试探究并解答：

    （3）求代数式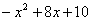的最大（或最小）值，并写出相应的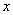的值．

    （4）求代数式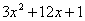的最大（或最小）值，并写出相应的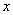的值．

    （5）已知，且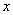的值在数1～4（包含1和4）之间变化，求这时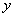的变化范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知，如图在矩形ABCD中，AD=6，DC=7，菱形EFGH的三个顶点E，G， H 分别在矩形ABCD的边AB ，CD ，AD 上，AH=2 ，连接CF.
    （1）当四边形EFGH为正方形时,求DG的长；
    （2）当△FCG的面积为1时,求DG的长；
    （3）当△FCG的面积最小时,求DG的长.

    .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某超市一月份的营业额为300万元，第一季度的营业额共为1500万元，如果平均每月增长率为，则由题意可列方程为(     )

    A．                     B．

    C．                  D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


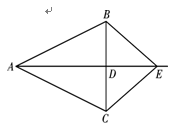    如图，在△ABC中，AB=AC，D是BC的中点，连结AD，在AD的延长线上取一点E，连结BE，CE.

    （1）求证：△ABE≌△ACE

    （2）当AE与AD满足什么数量关系时，四边形ABEC是菱形？

    并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    9.6   解：∵四边形ABCD是平行四边形（已知），

    ∴OA=OC（平行四边形的对角线相互平分），AB∥CD（平行四边形的对边相互平行），

    ∴∠DCO=∠BAC（两直线平行，内错角相等）；

    在△AFO和△CEO中，

    ，

    则△AFO≌△CEO（ASA），

    ∴OF=OE，CE=AF（全等三角形的对应边相等）；

    又∵AD=BC（平行四边形的对边相等），AB=4，AD=3，OF=1.3，

    ∴四边形BCEF的周长为：BC+EC+OE+OF+BF=AD+AF+2OF+BF=AD+AB+2OF=9.6；

    故答案是：9.6．

    查看答案和解析>>

    同步练习册答案