
已知,在平面直角坐标系中,A(a,0)、B(0,b),a、b满足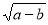 +|a?3
+|a?3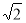 |=0.C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
|=0.C为AB的中点,P是线段AB上一动点,D是x轴正半轴上一点,且PO=PD,DE⊥AB于E.
(1)求∠OAB的度数;
(2)设AB=6,当点P运动时,PE的值是否变化?若变化,说明理由;若不变,请求PE的值;
(3)设AB=6,若∠OPD=45°,求点D的坐标.
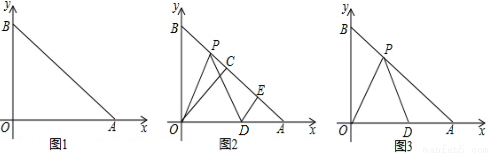
(1) 45°;(2)PE的值不变,PE=3;(3)D(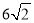 ?6,0).
?6,0).
【解析】
试题分析:(1)根据非负数的性质即可求得a,b的值,从而得到△AOB是等腰直角三角形,据此即可求得;
(2)根据等腰三角形的性质以及三角形的外角的性质可以得到∠POC=∠DPE,即可证得△POC≌△DPE,则OC=PE,OC的长度根据等腰直角三角形的性质可以求得;
(3)利用等腰三角形的性质,以及外角的性质证得∠POC=∠DPE,即可证得△POC≌△DPE,根据全等三角形的对应边相等,即可求得OD的长,从而求得D的坐标.
试题解析:(1)根据题意得:
 ,
,
解得:a=b= ,
,
∴OA=OB,
又∵∠AOB=90°
∴△AOB为等腰直角三角形,
∴∠OAB=45°.
(2)PE的值不变.理由如下:
∵△AOB为等腰直角三角形,且AC=BC,
∴∠AOC=∠BOC=45°
又∵OC⊥AB于C,
∵PO=PD
∴∠POD=∠PDO
又∵∠POD=45°+∠POC∠PDO=45°+∠DPE,
∴∠POC=∠DPE
在△POC和△DPE中,

∴△POC≌△DPE,
∴OC=PE
又OC=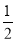 AB=3
AB=3
∴PE=3;
(3)∵OP=PD,
∴∠POD=∠PDO=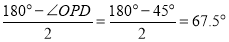 ,
,
则∠PDA=180°-∠PDO=180°-67.5°=112.5°,
∵∠POD=∠A+∠APD,
∴∠APD=67.5°-45°=22.5°,
∴∠BPO=180°-∠OPD-∠APD=112.5°,
∴∠PDA=∠BPO
则在△POB和△DPA中,
 ,
,
∴△POB≌△DPA.
∴PA=OA=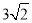 ,
,
∴DA=PB=6-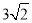 ,
,
∴OD=OA-DA=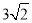 -(6-
-(6-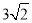 )=
)=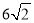 -6
-6
∴D(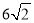 ?6,0).
?6,0).
考点:1.全等三角形的判定与性质;2.坐标与图形性质;3.等腰直角三角形.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源:2015届甘肃省八年级下学期期末考试数学试卷(解析版) 题型:填空题
如图,直线y=kx+b经过A(﹣1,1)和B(﹣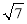 ,0)两点,则不等式0<kx+b<﹣x的解集为 .
,0)两点,则不等式0<kx+b<﹣x的解集为 .
查看答案和解析>>
科目:初中数学 来源:2015届湖南长沙麓山国际实验学校八年级下学期期中数学试卷(解析版) 题型:选择题
下列命题中,正确的是( )
A、经过两点只能作一个圆
B、垂直于弦的直径平分弦所对的两条弧
C、圆是轴对称图形,任意一条直径是它的对称轴
D、平分弦的直径必平分弦所对的两条弧
查看答案和解析>>
科目:初中数学 来源:2015届湖南省邵阳市八年级下学期期末考试数学试卷(解析版) 题型:选择题
要了解八年级学生身高在某一范围内学生所占比例,需知道相应的( )
A.平均数 B.众数 C.中位数 D.频数
查看答案和解析>>
科目:初中数学 来源:2015届湖北随州府河镇中心校八年级下学期期中考试数学试卷(解析版) 题型:解答题
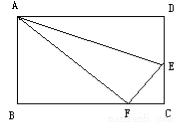
如图所示,折叠长方形一边AD,点D落在BC边的点F处,已知BC=10厘米,AB=8厘米,求FC的长。
查看答案和解析>>
科目:初中数学 来源:2015届湖北随州府河镇中心校八年级下学期期中考试数学试卷(解析版) 题型:填空题
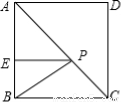
如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是______________
查看答案和解析>>
科目:初中数学 来源:2015届湖北省鄂州市梁子湖区八年级下学期联考数学试卷(解析版) 题型:解答题
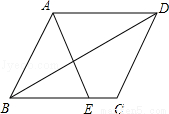
如图,在平行四边形ABCD中,E为BC边上的一点,连结AE、BD且AE=AB.
(1)求证:∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com