Question

【题目】如图，在平行四边形ABCD中，AB=4，∠BAD的平分线与BC的延长线交于点E，与DC交于点F，且点F为边DC的中点，DG⊥AE，垂足为G，若DG=1，则AE的边长为（ ）
A.2
B.4
C.4
D.8

Answer 1

【答案】B
【解析】解：∵AE为∠DAB的平分线， ∴∠DAE=∠BAE，
∵DC∥AB，
∴∠BAE=∠DFA，
∴∠DAE=∠DFA，
∴AD=FD，
又F为DC的中点，
∴DF=CF，
∴AD=DF= DC= AB=2，
在Rt△ADG中，根据勾股定理得：AG= ，
则AF=2AG=2 ，
∵平行四边形ABCD，
∴AD∥BC，
∴∠DAF=∠E，∠ADF=∠ECF，
在△ADF和△ECF中，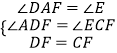
，
∴△ADF≌△ECF（AAS），
∴AF=EF，
则AE=2AF=4 ．
故选：B
由AE为角平分线，得到一对角相等，再由ABCD为平行四边形，得到AD与BE平行，利用两直线平行内错角相等得到一对角相等，等量代换及等角对等边得到AD=DF，由F为DC中点，AB=CD，求出AD与DF的长，得出三角形ADF为等腰三角形，根据三线合一得到G为AF中点，在直角三角形ADG中，由AD与DG的长，利用勾股定理求出AG的长，进而求出AF的长，再由三角形ADF与三角形ECF全等，得出AF=EF，即可求出AE的长．