
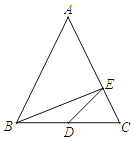
【题目】如图,在△ABC中,AB=AC,BC=6,E为AC边上的点且AE=2EC,点D在BC边上且满足BD=DE,设BD=y,S△ABC=x,则y与x的函数关系式为( )
A.y=![]() x2+
x2+![]() B.y=
B.y=![]() x2+
x2+![]()
C.y=![]() x2+2D.y=
x2+2D.y=![]() x2+2
x2+2
科目:初中数学 来源: 题型:
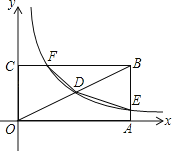
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,反比例函数![]() (x>0)在第一象限内的图象经过点D,且与AB、BC分别交于E、F两点,若四边形BEDF的面积为1,则k的值为_____.
(x>0)在第一象限内的图象经过点D,且与AB、BC分别交于E、F两点,若四边形BEDF的面积为1,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,平面直角坐标系中,矩形OABC的顶点B的坐标为(7,5),顶点A,C分别在x轴,y轴上,点D的坐标为(0,1),过点D的直线与矩形OABC的边BC交于点G,且点G不与点C重合,以DG为一边作菱形DEFG,点E在矩形OABC的边OA上,设直线DG的函数表达式为y=kx+b
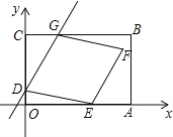
(1)当CG=OD时,求直线DG的函数表达式;
(2)当点E的坐标为(5,0)时,求直线DG的函数表达式;
(3)连接BF,设△FBG的面积为S,CG的长为a,请直接写出S与a的函数表达式及自变量a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接2019年中考,某中学对全校九年级学生进行了一次数学模拟考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如下两幅不完整的统计图,请根据图中的信息,解答下列问题;
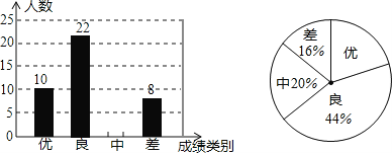
(1)本次调查中共抽查了______名学生,扇形统计图中表示成绩类别为“优”的扇形所对应的圆心角是______度;
(2)请补全条形统计图;
(3)若该中学九年级共有学生520人,请你估计该校九年级约有多少名学生的数学成绩可以达到优秀?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知m,n分别是关于x的一元二次方程ax2+bx+c=a与ax2+bx+c=b的一个根,且m=n+1.
(1)当m=2,a=﹣1时,求b与c的值;
(2)用只含字母a,n的代数式表示b;
(3)当a<0时,函数y=ax2+bx+c满足b2﹣4ac=a,b+c≥2a,n≤﹣![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
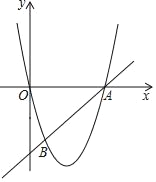
【题目】如图,在平面直角坐标系xOy中,直线AB与抛物线y=ax2+bx交于点A(6,0)和点B(1,﹣5).
(1)求这条抛物线的表达式和直线AB的表达式;
(2)如果点C在直线AB上,且∠BOC的正切值是![]() ,求点C的坐标.
,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
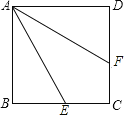
【题目】如图,四边形ABCD是正方形,点E、F分别在线段BC、DC上,线段AE绕点A逆时针旋转后与线段AF重合.若![]() ,则旋转的角度是( )
,则旋转的角度是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
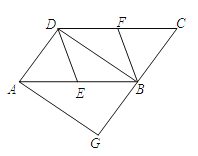
【题目】已知:如图,在![]() 中,
中,![]() 分别在边
分别在边![]() 的中点,
的中点,![]() 是对角线,过点
是对角线,过点![]() 作
作![]() ,交
,交![]() 的延长线于
的延长线于![]() .
.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若四边形![]() 是矩形,则四边形
是矩形,则四边形![]() 是什么特殊四边形?并证明你的结论.
是什么特殊四边形?并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com