
如图,二次函数 的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2),过A,C画直线.
的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2),过A,C画直线.
(1)求二次函数的解析式;
(2)点P在x轴正半轴上,且PA=PC,求OP的长;
(3)点M在二次函数图象上,以M为圆心的圆与直线AC相切,切点为H.
①若M在y轴右侧,且△CHM∽△AOC(点C与点A对应),求点M的坐标;
②若⊙M的半径为  ,求点M的坐标.
,求点M的坐标.

(1)抛物线的解析式为y=x2﹣x﹣2;
(2)OP= ;
;
(3)①M′( ,
, ),
),
②点M的坐标为( ,3+
,3+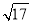 )或(
)或( ,3﹣
,3﹣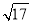 ).
).
【解析】
试题分析:(1)根据与x轴的两个交点A、B的坐标,设出二次函数交点式解析式y=a(x+1)(x﹣2),然后把点C的坐标代入计算求出a的值,即可得到二次函数解析式;
(2)设OP=x,然后表示出PC、PA的长度,在Rt△POC中,利用勾股定理列式,然后解方程即可;
(3)①根据相似三角形对应角相等可得∠MCH=∠CAO,然后分(i)点H在点C下方时,利用同位角相等,两直线平行判定CM∥x轴,从而得到点M的纵坐标与点C的纵坐标相同,是﹣2,代入抛物线解析式计算即可;(ii)点H在点C上方时,根据(2)的结论,点M为直线PC与抛物线的另一交点,求出直线PC的解析式,与抛物线的解析式联立求解即可得到点M的坐标;
②在x轴上取一点D,过点D作DE⊥AC于点E,可以证明△AED和△AOC相似,根据相似三角形对应边成比例列式求解即可得到AD的长度,然后分点D在点A的左边与右边两种情况求出OD的长度,从而得到点D的坐标,再作直线DM∥AC,然后求出直线DM的解析式,与抛物线解析式联立求解即可得到点M的坐标.
试题解析:(1)设该二次函数的解析式为:y=a(x+1)(x﹣2),
将x=0,y=﹣2代入,得﹣2=a(0+1)(0﹣2),
解得a=1,
∴抛物线的解析式为y=(x+1)(x﹣2),
即y=x2﹣x﹣2;
(2)设OP=x,则PC=PA=x+1,
在Rt△POC中,由勾股定理,得x2+22=(x+1)2,
解得,x= ,
,
即OP= ;
;
(3)①∵△CHM∽△AOC,
∴∠MCH=∠CAO,
(i)如图1,当H在点C下方时,
∵∠OAC+∠OCA=90°,∠MCH=∠OAC
∴∠OCA+∠MCH=90°
∴∠OCM=90°=∠AOC
∴CM∥x轴
∴yM=﹣2,
∴x2﹣x﹣2=﹣2,
解得x1=0(舍去),x2=1,
∴M(1,﹣2),
(ii)如图1,当H在点C上方时,
∵∠MCH=∠CAO,
∴PA=PC,由(2)得,M′为直线CP与抛物线的另一交点,
设直线CM的解析式为y=kx﹣2,
把P( ,0)的坐标代入,得
,0)的坐标代入,得 k﹣2=0,
k﹣2=0,
解得k= ,
,
∴y= x﹣2,
x﹣2,
由 x﹣2=x2﹣x﹣2,
x﹣2=x2﹣x﹣2,
解得x1=0(舍去),x2= ,
,
此时y= ×
× ﹣2=
﹣2= ,
,
∴M′( ,
, ),
),
②在x轴上取一点D,如图(备用图),过点D作DE⊥AC于点E,使DE= ,
,
在Rt△AOC中,AC= =
=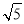 ,
,
∵∠COA=∠DEA=90°,∠OAC=∠EAD,
∴△AED∽△AOC,
∴ ,
,
解得AD=2,
∴D(1,0)或D(﹣3,0).
过点D作DM∥AC,交抛物线于M,如图(备用图)
则直线DM的解析式为:y=﹣2x+2或y=﹣2x﹣6,
当﹣2x﹣6=x2﹣x﹣2时,即x2+x+4=0,方程无实数根,
当﹣2x+2=x2﹣x﹣2时,即x2+x﹣4=0,解得x1= ,x2=
,x2= ,
,
∴点M的坐标为( ,3+
,3+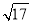 )或(
)或( ,3﹣
,3﹣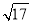 ).
).


考点:二次函数综合题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源:2013-2014学年江苏省无锡市崇安区九年级下学期期中统考(一模)数学试卷(解析版) 题型:填空题
已知函数y=2x-b的图象经过点(1,b),则b的值为 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市崇安区九年级下学期期中统考(一模)数学试卷(解析版) 题型:选择题
若a2-b2= ,a-b=
,a-b= ,则a+b的值为( )
,则a+b的值为( )
A.- B.
B. C.1 D.2
C.1 D.2
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市宜兴外国语学校九年级下学期期中考试数学试卷(解析版) 题型:解答题
(本题满分8分)吸烟有害健康,为配合“戒烟”运动,某校组织同学们在社区开展了“你支持哪种戒烟方式”的随机问卷调查,并将调查结果绘制成两幅不完整的统计图:

根据统计图解答下列问题:
(1)同学们一共调查了 人?
(2)将条形统计图补充完整。
(3)若该社区有1万人,请你估计大约有多少人支持“警示戒烟”这种方式?
(4)为了让更多的市民增强“戒烟”意识,同学们在社区做了两期“警示戒烟”的宣传。在(3)的条件下,若每期宣传后,市民支持“警示戒烟”的平均增长率为20%,则两期宣传后支持“警示戒烟”的市民约有多少人?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市宜兴外国语学校九年级下学期期中考试数学试卷(解析版) 题型:填空题
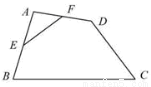
如图,在四边形ABCD中,E、F分别是AB、AD的中点。若EF=2,BC=5,CD=3,则tan C等于 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市九年级3月阶段测试数学试卷(解析版) 题型:解答题
如图, 点
点 在
在 轴的正半轴上,
轴的正半轴上, ,
, ,
, .点
.点 从点
从点 出发,沿
出发,沿 轴向左以每秒1个单位长的速度运动,运动时间为
轴向左以每秒1个单位长的速度运动,运动时间为 秒.
秒.

(1)求点 的坐标;
的坐标;
(2)当 时,求
时,求 的值;
的值;
(3)以点 为圆心,
为圆心, 为半径的
为半径的 随点
随点 的运动而变化,当
的运动而变化,当 与四边形
与四边形 的边(或边所在的直线)相切时,求
的边(或边所在的直线)相切时,求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com