
如图, 点
点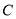 在
在 轴的正半轴上,
轴的正半轴上, ,
, ,
, .点
.点 从点
从点 出发,沿
出发,沿 轴向左以每秒1个单位长的速度运动,运动时间为
轴向左以每秒1个单位长的速度运动,运动时间为 秒.
秒.

(1)求点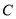 的坐标;
的坐标;
(2)当 时,求
时,求 的值;
的值;
(3)以点 为圆心,
为圆心, 为半径的
为半径的 随点
随点 的运动而变化,当
的运动而变化,当 与四边形
与四边形 的边(或边所在的直线)相切时,求
的边(或边所在的直线)相切时,求 的值.
的值.
(1)点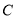 的坐标为(0,3);
的坐标为(0,3);
(2)t的值为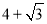 或
或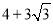 ;
;
(3)t的值为1或4或5.6.
【解析】
试题分析:(1)由∠CBO=45°,∠BOC为直角,得到△BOC为等腰直角三角形,又OB=3,利用等腰直角三角形AOB的性质知OC=OB=3,然后由点C在y轴的正半轴可以确定点C的坐标;
(2)需要对点P的位置进行分类讨论:①当点P在点B右侧时,求出此时的时间t;②当点P在点B左侧时,求出此时的时间t;
(3)当⊙P与四边形ABCD的边(或边所在的直线)相切时,分三种情况考虑:
①当⊙P与BC边相切时,得出此时的时间t;
②当⊙P与CD相切于点C时,P与O重合,可得出P运动的路程为OQ的长,求出此时的时间t;
③当⊙P与CD相切时,得到此时的时间t.
综上,得到所有满足题意的时间t的值.
试题解析:(1)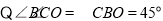 ,
,
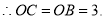
又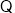 点
点 在
在 轴的正半轴上,
轴的正半轴上,
 点
点 的坐标为(0,3);
的坐标为(0,3);
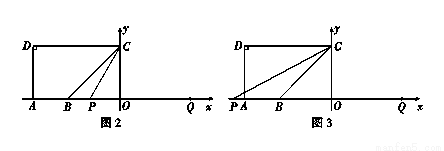
(2)当点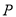 在点
在点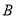 右侧时,如图2.
右侧时,如图2.
若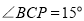 ,得
,得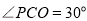 .
.
故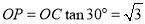 ,此时
,此时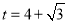 .
.
当点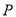 在点
在点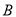 左侧时,如图3,由
左侧时,如图3,由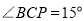 ,
,
得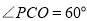 ,故
,故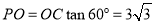 .
.
此时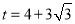 .
.
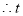 的值为
的值为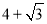 或
或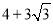 ;
;

(3)由题意知,若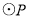 与四边形
与四边形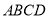 的边相切,有以下三种情况:
的边相切,有以下三种情况:
①当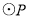 与
与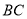 相切于点
相切于点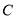 时,有
时,有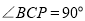 ,从而
,从而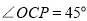 得到
得到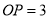 .
.
此时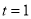 .
.
②当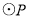 与
与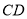 相切于点
相切于点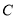 时,有
时,有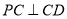 ,即点
,即点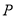 与点
与点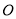 重合,
重合,
此时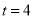 .
.
③当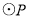 与
与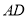 相切时,由题意,
相切时,由题意,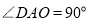 ,
,
 点
点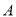 为切点,如图4.
为切点,如图4.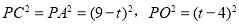 .
.
于是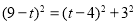 .解出
.解出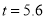 .
.
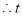 的值为1或4或5.6.
的值为1或4或5.6.
考点:1.切线的性质2.坐标与图形性质3.勾股定理4.解直角三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2013-2014学年江苏省无锡市宜兴外国语学校九年级下学期期中考试数学试卷(解析版) 题型:解答题
如图,二次函数 的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2),过A,C画直线.
的图象交x轴于A(﹣1,0),B(2,0),交y轴于C(0,﹣2),过A,C画直线.
(1)求二次函数的解析式;
(2)点P在x轴正半轴上,且PA=PC,求OP的长;
(3)点M在二次函数图象上,以M为圆心的圆与直线AC相切,切点为H.
①若M在y轴右侧,且△CHM∽△AOC(点C与点A对应),求点M的坐标;
②若⊙M的半径为  ,求点M的坐标.
,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市宜兴外国语学校九年级下学期期中考试数学试卷(解析版) 题型:选择题
⊙O的半径为8,圆心O到直线l的距离为4,则直线l与⊙O的位置关系是( )
A.相切 B.相交 C.相离 D.不能确定
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市九年级3月阶段测试数学试卷(解析版) 题型:解答题
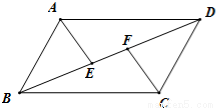
如图,在 ABCD中,E、F为对角线BD上的两点,且∠BAE=∠DCF.求证:BE=DF.
ABCD中,E、F为对角线BD上的两点,且∠BAE=∠DCF.求证:BE=DF.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市九年级3月阶段测试数学试卷(解析版) 题型:填空题
在一次体检中,测得某小组5名同学的身高分别是170、162、155、160、168(单位:厘米),则这组数据的极差是 厘米.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省扬州市邗江区九年级中考一模数学试卷(解析版) 题型:解答题
某厂工人小宋某月工作部分信息如下。
信息一:工作时间:每天上午8:00—12:00,下午14:00—18:00,每月20天
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品件数不少于60件。生产产品的件数与所用时间之间的关系如下表:

信息三:按件数计酬,每生产一件甲产品可得1.5元,每生产一件乙产品可得2.8元。
信息四:小宋工作时两种产品不能同时进行生产。
根据以上信息回答下列问题:
小宋每生产一件甲种产品,每生产一件乙种产品分别需要多少时间?
小宋该月最多能得多少元?此时生产的甲、乙两种产品分别是多少件?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省张家港市九年级5月网上阅卷适应性考试数学试卷(解析版) 题型:填空题
现有五张完全相同的卡片,上面分别写有“中国”、“美国”、“韩国”、“德国”、“英国”,把卡片背面朝上洗匀,然后从中随机抽取一张,抽到卡片对应的国家为亚洲的概率是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com