
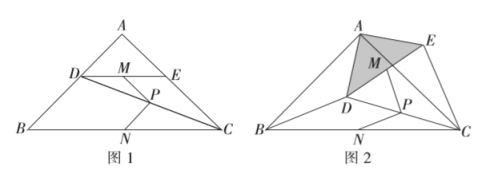
【题目】定义:既相等又垂直的两条线段称为“等垂线段”,如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,
上,![]() ,连接
,连接![]() 、
、![]() ,点
,点![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 的中点,且连接
的中点,且连接![]() 、
、![]() .
.
观察猜想
(1)线段![]() 与
与![]() “等垂线段”(填“是”或“不是”)
“等垂线段”(填“是”或“不是”)
猜想论证
(2)![]() 绕点
绕点![]() 按逆时针方向旋转到图2所示的位置,连接
按逆时针方向旋转到图2所示的位置,连接![]() ,
,![]() ,试判断
,试判断![]() 与
与![]() 是否为“等垂线段”,并说明理由.
是否为“等垂线段”,并说明理由.
拓展延伸
(3)把![]() 绕点
绕点![]() 在平面内自由旋转,若
在平面内自由旋转,若![]() ,
,![]() ,请直接写出
,请直接写出![]() 与
与![]() 的积的最大值.
的积的最大值.
【答案】(1)是;(2)是,理由详见解析;(3)49
【解析】
(1)根据题意,利用等腰三角形和三角形中位线定理得出![]() ,∠MPN=90°判定即可;
,∠MPN=90°判定即可;
(2)由旋转和三角形中位线的性质得出![]() ,再由中位线定理进行等角转换,得出∠MPN=90°,即可判定;
,再由中位线定理进行等角转换,得出∠MPN=90°,即可判定;
(3)由题意,得出![]() 最大时,
最大时,![]() 与
与![]() 的积最大,点
的积最大,点![]() 在
在![]() 的延长线上,再由(1)(2)结论,
的延长线上,再由(1)(2)结论,![]() 得出
得出![]() 与
与![]() 的积的最大值.
的积的最大值.
(1)是;
∵![]() ,
,![]()
∴DB=EC,∠ADE=∠AED=∠B=∠ACB
∴DE∥BC
∴∠EDC=∠DCB
∵点![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 的中点
的中点
∴PM∥EC,PN∥BD,![]()
∴![]() ,∠DPM=∠DCE,∠PNC=∠DBC
,∠DPM=∠DCE,∠PNC=∠DBC
∵∠DPN=∠PNC+∠DCB
∴∠MPN=∠DPM+∠DPN=∠ACD+∠DCB+∠B=180°-90°=90°
∴线段![]() 与
与![]() 是“等垂线段”;
是“等垂线段”;
(2)由旋转知![]()
∵![]() ,
,![]()
∴![]() ≌
≌![]() (
(![]() )
)
∴![]() ,
,![]()
利用三角形的中位线得![]() ,
,![]() ,
,
∴![]()
由中位线定理可得![]() ,
,![]()
∴![]() ,
,![]()
∵![]()
∴![]()
![]()
![]()
∵![]()
∴![]()
∴![]()
∴![]() 与
与![]() 为“等垂线段”;
为“等垂线段”;
(3)![]() 与
与![]() 的积的最大值为49;
的积的最大值为49;
由(1)(2)知,![]()
∴![]() 最大时,
最大时,![]() 与
与![]() 的积最大
的积最大
∴点![]() 在
在![]() 的延长线上,如图所示:
的延长线上,如图所示:
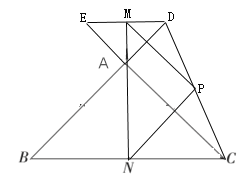
∴![]()
∴![]()
∴![]() .
.


科目:初中数学 来源: 题型:
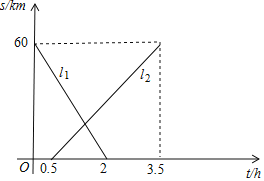
【题目】A,B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中l1,l2表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
(1)表示乙离A地的距离与时间关系的图象是 (填l1或l2);甲的速度是 km/h,乙的速度是 km/h;
(2)求出l1,l2的解析式,并标注自变量的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
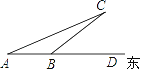
【题目】如图,一艘轮船以18海里/时的速度由西向东航行,在A处测得小岛C在北偏东75°方向上,两小时后,轮船在B处测得小岛C在北偏东60°方向上,在小岛周围15海里处有暗礁,若轮船仍然按18海里/时的速度向东航行,请问是否有触礁危险?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两工程队合作完成一项工程,需要12天完成,工程费用共36000元,若甲、乙两工程队单独完成此项工程,乙工程队所用的时间是甲工程队的1.5倍,乙工程队每天的费用比甲工程队少800元.
(1)问甲、乙两工程队单独完成此项工程各需多少天?
(2)若让一个工程队单独完成这项工程,哪个工程队的费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
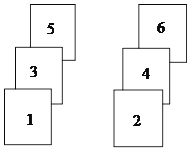
【题目】小明与小亮玩游戏,如图,两组相同的卡片,每组三张,第一组卡片正面分别标有数字1,3,5;第二组卡片正面分别标有数字2,4,6.他们将卡片背面朝上,分组充分洗匀后,从每组卡片中各摸出一张,称为一次游戏.当摸出的两张卡片的正面数字之积小于10,则小明获胜;当摸出的两张卡片的正面数字之积超过10,则小亮获胜.你认为这个游戏规则对双方公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
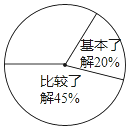
【题目】某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了不完整的表格和扇形统计图(如图).
等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
频数 | 50 | m | 40 | 20 |
根据以上提供的信息解答下列问题:
(1)本次问卷调查共抽取的学生数为多少人,表中m的值为多少;
(2)计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数,并补全扇形统计图;
(3)若该校有学生2000人,请根据调查结果估计这些学生中“不太了解”梅山文化知识的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王勇和李明两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了30次实验,实验的结果如下:
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 2 | 5 | 6 | 4 | 10 | 3 |
(1)分别计算这30次实验中“3点朝上”的频率和“5点朝上”的频率;
(2)王勇说:“根据以上实验可以得出结论:由于5点朝上的频率最大,所以一次实验中出现5点朝上的概率最大”;李明说:“如果投掷300次,那么出现6点朝上的次数正好是30次”.试分别说明王勇和李明的说法正确吗?并简述理由;
(3)现王勇和李明各投掷一枚骰子,请用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(1)求证:AEBC=BDAC;
(2)如果S△ADE=3,S△BDE=2,DE=6,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由同样大小的正方形按照一定规律所组成的,其中第①个图形中一个有2个正方形,第②个图形中一共有8个正方形,第③个图形中一共有16个正方形,…,按此规律,第⑦个图形中正方形的个数为( )

A. 56 B. 65 C. 68 D. 71
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com