
【题目】如图,AB是⊙O的直径,AE交⊙O于点F,且与⊙O的切线CD互相垂直,垂足为D.
(1)求证:∠EAC=∠CAB;
(2)若CD=4,AD=8,求⊙O的半径.

【答案】(1)证明见解析;(2)⊙O的半径为5.
【解析】试题分析:(1)首先连接OC,由CD是 O的切线,CD⊥OC,又由CD⊥AE,即可判定OC∥AE,根据平行线的性质与等腰三角形的性质,即可证得∠EAC=∠CAB;
(2)连接BC,易证得△ACD∽△ABC,根据相似三角形的对应边成比例,即可求得AB的长,继而可得⊙O的半径长.
(1)证明:连接OC.
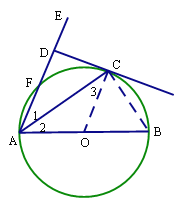
∵CD是⊙O的切线,
∴CD⊥OC,
又∵CD⊥AE,
∴OC∥AE,
∴∠1=∠3,
∵OC=OA,
∴∠2=∠3,
∴∠1=∠2,
即∠EAC=∠CAB;
(2)解:连接BC.
∵AB是⊙O的直径,CD⊥AE于点D,
∴∠ACB=∠ADC=90°,
∵∠1=∠2,
∴△ACD∽△ABC,
∴![]() ,
,
∵AC2=AD2+CD2=42+82=80,
∴AB=![]() =10,
=10,
∴⊙O的半径为10÷2=5.


科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广,为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写大赛”![]() 为了解本次大赛的成绩,校团委随机抽取了其中若干名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
为了解本次大赛的成绩,校团委随机抽取了其中若干名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
成绩 | 频数 | 频率 |
| 10 |
|
| 30 |
|
| 40 | n |
| m |
|
| 50 |
|
a | 1 |
请根据所给信息,解答下列问题:
![]() ______,
______,![]() ______,
______,![]() ______;
______;
![]() 补全频数直方图;
补全频数直方图;
![]() 这若干名学生成绩的中位数会落在______分数段;
这若干名学生成绩的中位数会落在______分数段;
![]() 若成绩在90分以上
若成绩在90分以上![]() 包括90分
包括90分![]() 的为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?
的为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
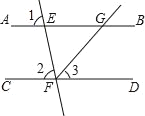
【题目】学习完第五章《相交线与平行线》后,王老师布置了一道儿何证明题如下:“如图,已知直线AB,CD被直线EF所截,FG平分∠EFD,∠1=∠2=80°,求∠BGF的度数.”善于动脑的小军快速思考,找到了解题方案,并书写出了如下不完整的解题过程.请你将该题解题过程补充完整:
解:∵∠1=∠2=80°(已知)
∴AB∥CD
∴∠BGF+∠3=180°
∵∠2+∠EFD=180°(邻补角的定义),
∴∠EFD= °(等式性质)
∵FG平分∠EFD(已知),
∴∠EFD=2∠3(角平分线的定义)
∴∠3= °(等式性质)
∴∠BGF= °(等式性质)
查看答案和解析>>
科目:初中数学 来源: 题型:
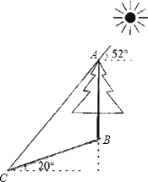
【题目】如图,在一个坡角为20°的斜坡上有一棵树,高为AB,当太阳光线与水平线成52°角时,测得该树斜坡上的树影BC的长为10m,求树高AB(精确到0.1m) (已知:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364,sin52°≈0.788,cos52°≈0.616,tan52°≈1.280.供选用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让市民享受到更多的优惠,相关部门拟确定一个折扣线,计划使50%左右的人获得折扣优惠.某市针对乘坐地铁的人群进行了调查.调查小组在各地铁站随机调查了该市1000人上一年乘坐地铁的月均花费(单位:元),绘制了频数分布直方图,如图所示.下列说法正确的是( )

①每人乘坐地铁的月均花费最集中的区域在80~100元范围内;
②每人乘坐地铁的月均花费的平均数范围是40~60元范围内;
③每人乘坐地铁的月均花费的中位数在60~100元范围内;
④乘坐地铁的月均花费达到80元以上的人可以享受折扣.
A.①②④B.①③④C.③④D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2-(m+2)x+2=0(m≠0)
(1)求证:方程一定有两个实数根;
(2)若此方程的两根为不相等的整数,求整数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,直线l3和直线l1,l2交于C、D两点,点P在直线CD上.
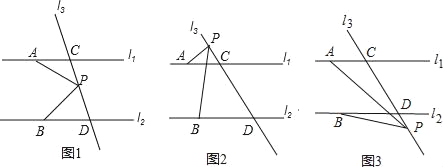
(1)试写出图1中∠APB、∠PAC、∠PBD之间的关系,并说明理由;
(2)如果P点在C、D之间运动时,∠APB、∠PAC、∠PBD之间的关系会发生变化吗?
答: (填发生或不发生)
(3)若点P在C、D两点的外侧运动时(P点与点C、D不重合),如图2,图3,试分別写出∠PAC、∠APB、∠PBD之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
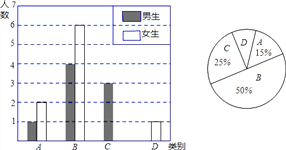
【题目】我县实施新课程改革后,学生的自主学习、合作交流能力有很大提高,胡老师为了了解班级学生自主学习、合作交流的具体情况,对某班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)本次调查中,胡老师一共调查了 名同学,其中女生共有 ___名;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,胡老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com