
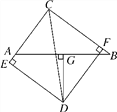
【题目】如图,已知在△ABC中,AC=6,BC=8,AB=10,∠BCA的平分线与AB边的垂直平分线相交于点D,DE⊥AC,DF⊥BC,DG⊥AB,垂足分别是E,F,G.
(1)求证:AE=BF;
(2)求AE的长.
【答案】(1)证明见解析;(2))AE=1.
【解析】(1)根据中垂线、角平分线的性质来证明Rt△DEA≌Rt△DFB,然后根据全等三角形的对应边相等推知AE=BF;
(2)设AE=BF=x,根据HL可证得Rt△CDE≌Rt△CDF,根据全等三角形对应边相等可得CE=CF,可得关于x的方程,解方程即可得.
(1)如图,连接AD,BD,
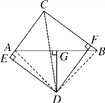
∵CD为∠BCA的平分线,∴∠DCE=∠DCB,
又∵DE⊥CA,DF⊥CB,∴DE=DF,∠AED=∠DFB=90°,
∵DG垂直平分AB,∴DA=DB,
在Rt△DEA和Rt△DFB中,
![]() ,
,
∴Rt△DEA≌Rt△DFB,
∴AE=BF;
(2)设AE=BF=x,
在Rt△CDE和Rt△CDF中,
![]() ,
,
∴Rt△CDE≌Rt△CDF,
∴CE=CF,
∴6+x=8-x,
∴x=1,∴AE=1.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,小华同学设计了一个圆的直径的测量器.标有刻度的两把尺子OA,OB在O点被钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,尺子OA与圆交于点F,尺子OB与圆交于点E,读得OF为8个单位长度,OE为6个单位长度.则圆的直径为( ) 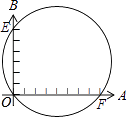
A.25个单位长度
B.14个单位长度
C.12个单位长度
D.10个单位长度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )

A. BD=CD B. ∠BAD=∠CAD C. ∠B=∠C D. ∠ADB=∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC和△MNB中,∠ACB=∠MBN=90°,AC=BC=4,MB=NB= ![]() BC,点N在BC边上,连接AN,CM,点E,F,D,G分别为AC,AN,MN,CM的中点,连接EF,FD,DG,EG.
BC,点N在BC边上,连接AN,CM,点E,F,D,G分别为AC,AN,MN,CM的中点,连接EF,FD,DG,EG. 
(1)判断四边形EFDG的形状,并证明;
(2)如图2,将图1中的△MBN绕点B逆时针旋转90°,其他条件不变,猜想此时四边形EFDG的形状,并证明. 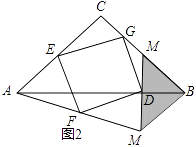
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.
(1)求证:△ABP≌△ACQ;
(2)请判断△APQ是什么三角形,试说明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某加工厂以每吨3000元的价格购进50吨原料进行加工.若进行粗加工,每吨加工费用为600元,需 ![]() 天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需
天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需 ![]() 天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
(1)请完成表格并求出y与x的函数关系式(不要求写自变量的范围); 表一
粗加工数量/吨 | 3 | 7 | x |
精加工数量/吨 | 47 |
表二
粗加工数量/吨 | 3 | 7 | x |
粗加工获利/元 | 2800 | ||
精加工获利/元 | 25800 |
y与x的函数关系式
(2)如果必须在20天内完成,如何安排生产才能获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂一周计划每日生产某产品100吨,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的吨数记为正数,减少的吨数记为负数)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减/吨 | ﹣1 | +3 | ﹣2 | +4 | +7 | ﹣5 | ﹣10 |
(1)生产量最多的一天比生产量最少的一天多生产多少吨?
(2)本周总生产量是多少吨?比原计划增加了还是减少了?增减数为多少吨?
(3)若本周总生产的产品全部由35辆货车一次性装载运输离开工厂,则平均每辆货车大约需装载多少吨?(结果精确到0.01吨)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,反比例函数y= ![]() 的图像与正比例函数y=kx(k≠0)的图像相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0).
的图像与正比例函数y=kx(k≠0)的图像相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0). 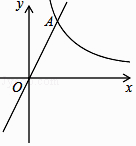
(1)求平移后直线的表达式;
(2)求OA平移后所得直线与双曲线的交点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com