
【题目】已知,点M是二次函数y=ax2(a>0)图象上的一点,点F的坐标为(0, ![]() ),直角坐标系中的坐标原点O与点M,F在同一个圆上,圆心Q的纵坐标为
),直角坐标系中的坐标原点O与点M,F在同一个圆上,圆心Q的纵坐标为 ![]() .
.
(1)求a的值;
(2)当O,Q,M三点在同一条直线上时,求点M和点Q的坐标;
(3)当点M在第一象限时,过点M作MN⊥x轴,垂足为点N,求证:MF=MN+OF.
【答案】
(1)
解:∵圆心O的纵坐标为 ![]() ,
,
∴设Q(m, ![]() ),F(0,
),F(0, ![]() ),
),
∵QO=QF,
∴m2+( ![]() )2=m2+(
)2=m2+( ![]() ﹣
﹣ ![]() )2,
)2,
∴a=1,
∴抛物线为y=x2
(2)
解:∵M在抛物线上,设M(t,t2),Q(m, ![]() ),
),
∵O、Q、M在同一直线上,
∴KOM=KOQ,
∴ ![]() =
= ![]() ,
,
∴m= ![]() ,
,
∵QO=QM,
∴m2+( ![]() )2=(m﹣t)2=(
)2=(m﹣t)2=( ![]() ﹣t2)2,
﹣t2)2,
整理得到:﹣ ![]() t2+t4+t2﹣2mt=0,
t2+t4+t2﹣2mt=0,
∴4t4+3t2﹣1=0,
∴(t2+1)(4t2﹣1)=0,
∴t1= ![]() ,t2=﹣
,t2=﹣ ![]() ,
,
当t1= ![]() 时,m1=
时,m1= ![]() ,
,
当t2=﹣ ![]() 时,m2=﹣
时,m2=﹣ ![]() .
.
∴M1( ![]() ,
, ![]() ),Q1(
),Q1( ![]() ,
, ![]() ),M2(﹣
),M2(﹣ ![]() ,
, ![]() ),Q2(﹣
),Q2(﹣ ![]() ,
, ![]() )
)
(3)
解:设M(n,n2)(n>0),
∴N(n,0),F(0, ![]() ),
),
∴MF= ![]() =n2+
=n2+ ![]() ,MN+OF=n2+
,MN+OF=n2+ ![]() ,
,
∴MF=MN+OF.
【解析】(1)设Q(m, ![]() ),F(0,
),F(0, ![]() ),根据QO=QF列出方程即可解决问题.(2)设M(t,t2),Q(m,
),根据QO=QF列出方程即可解决问题.(2)设M(t,t2),Q(m, ![]() ),根据KOM=KOQ , 求出t、m的关系,根据QO=QM列出方程即可解决问题.(3)设M(n,n2)(n>0),则N(n,0),F(0,
),根据KOM=KOQ , 求出t、m的关系,根据QO=QM列出方程即可解决问题.(3)设M(n,n2)(n>0),则N(n,0),F(0, ![]() ),利用勾股定理求出MF即可解决问题.本题考查二次函数的应用、三点共线的条件、勾股定理等知识,解题的关键是设参数解决问题,把问题转化为方程解决,属于中考常考题型.
),利用勾股定理求出MF即可解决问题.本题考查二次函数的应用、三点共线的条件、勾股定理等知识,解题的关键是设参数解决问题,把问题转化为方程解决,属于中考常考题型.


科目:初中数学 来源: 题型:
【题目】下表中有两种移动电话计费方式.
月使用费 | 主叫限定时间 | 主叫超时费 | 被叫 | |
方式一 | 49 | 100 |
| 免费 |
方式二 | 69 | 150 |
| 免费 |
设一个月内主叫通话为t分钟![]() 是正整数
是正整数![]() .
.
![]() 当
当![]() 时,按方式一计费为______元;按方式二计费为______元;
时,按方式一计费为______元;按方式二计费为______元;
![]() 当
当![]() 时,是否存在某一时间t,使两种计费方式相等,若存在,请求出对应t的值,若不存在,请说明理由;
时,是否存在某一时间t,使两种计费方式相等,若存在,请求出对应t的值,若不存在,请说明理由;
![]() 当
当![]() 时,请直接写出省钱的计费方式?
时,请直接写出省钱的计费方式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为16,点D是BC边上一点,且BD= ![]() BC,点G是AB上一点,点H在△ABC内部,且四边形BDHG是平行四边形,则图中阴影部分的面积是( )
BC,点G是AB上一点,点H在△ABC内部,且四边形BDHG是平行四边形,则图中阴影部分的面积是( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y= ![]() (a>0,a为常数)和y=
(a>0,a为常数)和y= ![]() 在第一象限内的图象如图所示,点M在y=
在第一象限内的图象如图所示,点M在y= ![]() 的图象上,MC⊥x轴于点C,交y=
的图象上,MC⊥x轴于点C,交y= ![]() 的图象于点A;MD⊥y轴于点D,交y=
的图象于点A;MD⊥y轴于点D,交y= ![]() 的图象于点B,当点M在y=
的图象于点B,当点M在y= ![]() 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①S△ODB=S△OCA;
②四边形OAMB的面积不变;
③当点A是MC的中点时,则点B是MD的中点.
其中正确结论的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,点A、B、C都是格点.
(1)将△ABC向左平移6个单位长度得到△A 1B 1C 1,请在网格中画出△A 1B 1C 1
(2)将△ABC绕点O按逆时针方向旋转180°得到△A 2B 2C 2,请在网格画出△A 2B 2C 2.
(3)请问△A 1B 1C 1与△A 2B 2C 2成中心对称吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对下列代数式作出解释,其中不正确的是( )
A. a-b:今年小明b岁,小明的爸爸a岁,小明比他爸爸小(a-b)岁
B. a-b:今年小明b岁,小明的爸爸a岁,则小明出生时,他爸爸为(a-b)岁
C. ab:长方形的长为acm,宽为bcm,长方形的面积为ab ![]()
D. ab:三角形的一边长为acm,这边上的高为bcm,此三角形的面积为ab ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数![]() ,下列说法不正确的是( )
,下列说法不正确的是( )
A. 点(-2,-1)在它的图像上 B. 它的图像在第一、三象限
C. 当![]() 时,y随x的增大而增大 D. 当
时,y随x的增大而增大 D. 当![]() 时,y随x的增大而减小
时,y随x的增大而减小
【答案】C
【解析】试题分析:反比例函数![]() 的性质:当
的性质:当![]() 时,图象在一、三象限,在每一象限,y随x的增大而减小;当
时,图象在一、三象限,在每一象限,y随x的增大而减小;当![]() 时,图象在二、四象限,在每一象限,y随x的增大而增大.
时,图象在二、四象限,在每一象限,y随x的增大而增大.
A.点![]() 在它的图象上,B.它的图象在第一、三象限,C.当
在它的图象上,B.它的图象在第一、三象限,C.当![]() 时,
时,![]() 随
随![]() 的增大而减小,均正确,不符合题意;
的增大而减小,均正确,不符合题意;
D.当![]() 时,
时,![]() 随
随![]() 的增大而减小,故错误,本选项符合题意.
的增大而减小,故错误,本选项符合题意.
考点:反比例函数的性质
点评:本题属于基础应用题,只需学生熟练掌握反比例函数的性质,即可完成.
【题型】单选题
【结束】
8
【题目】如图,双曲线![]() (x<0)经过平行四边形ABCO的对角线交点D,已知边OC在y轴上,且AC⊥AB于点C,则平行四边形ABCO的面积是( )
(x<0)经过平行四边形ABCO的对角线交点D,已知边OC在y轴上,且AC⊥AB于点C,则平行四边形ABCO的面积是( )

A. ![]() B.
B. ![]() C. 3 D. 6
C. 3 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图①,在正方形ABCD中,点P在边CD上(不与点C、D重合),连接BP,将△BCP绕点C顺时针旋转至△DCE,点B的对应点是点D.旋转的角度是 度.应用:将图①中的BP延长交边DE于点F,其它条件不变,如图②,求∠BFE的度数。拓展:如图②,若DP=2CP,BC=6,则四边形ABED的面积是 .
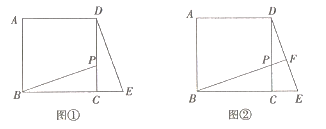
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图□ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=600,AB=![]() BC,连接OE .下列 结论:①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=
BC,连接OE .下列 结论:①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=![]() BC 成立的个数有( )
BC 成立的个数有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com