
【题目】元宵节将至,我校组织学生制作并选送50盏花灯,共包括传统花灯、创意花灯和现代花灯三大种.已知每盏传统花灯需要35元材料费,每盏创意花灯需要33元材料费,每盏现代花灯需要30元材料费.
(1)如果我校选送20盏现代花灯,已知传统花灯数量不少于5盏且总材料费不得超过1605元,请问选送传统花灯、创意花灯的数量有哪几种方案?
(2)当三种花灯材料总费用为1535元时,求选送传统花灯、创意花灯、现代花灯各几盏?
【答案】(1)答案见解析;(2)答案见解析.
【解析】
(1)设该校选送传统花灯x盏,则创意花灯(30-x)盏,根据总材料费不得超过1605元可得关于x的不等式,再结合x≥5且x为正整数,可求得x=5或6或7,继而可得答案;
(2)设选送传统花灯a盏,创意花灯b盏,则现代花灯(50-a-b)盏,由总材料费为1535元可得关于a、b的方程,继而根据a、b为正整数即可求得答案.
(1)设该校选送传统花灯x盏,则创意花灯(30-x)盏,
依题意,得:35x+33(30-x)+20×30≤1605,
解得x≤7.5,
∵x≥5且x为正整数,∴取x=5或6或7,
有三种方案:
①当x=5时,该校选送传统花灯5盏,创意花灯25盏;
②当x=6时,该校选送传统花灯6盏,创意花灯24盏;
③当x=7时,该校选送传统花灯7盏,创意花灯23盏;
(2)设选送传统花灯a盏,创意花灯b盏,则现代花灯(50-a-b)盏,
依题意,得:35a+33b+30(50-a-b)=1535,
![]() ,
,
解得5a+3b=35,即
∵a、b必须为正整数,
∴b应取5的倍数,即b=5或10,
方案一:当b=5,a=4时,即该校选送传统花灯4盏,创意花灯5盏,现代花灯41盏;
方案二:当b=10,a=1时,该校选送传统花灯1盏,创意花灯10盏,现代花灯39盏.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD//BC,∠B=70°,∠C=40°,DE//AB交BC于点E.若AD=3cm,BC=10cm,则CD的长是 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.
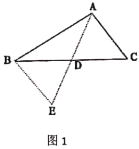
(1)如图1,若AE、CD为△ABC的角平分线:
①求∠AFD的度数;
②若AD=3,CE=2,求AC的长;
(2)如图2,若∠EAC=∠DCA=30°,求证:AD=CE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD= ![]() ,求AF的长.
,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
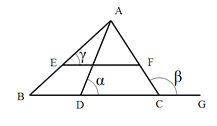
【题目】如图,在△ABC中,EF∥BC,∠ACG是△ABC的外角,∠BAC=3∠BAD,记∠ADC=![]() ,∠ACG=
,∠ACG=![]() ,∠AEF=
,∠AEF=![]() ,则:(1)
,则:(1)![]() __
__![]() (填“>”、“=”或“<”号);
(填“>”、“=”或“<”号);
(2)![]() 、
、![]() 、
、![]() 三者间的数量关系式是_______________.
三者间的数量关系式是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课外兴趣小组活动时,老师提出了如下问题:
(1)如图1,![]() 中,若
中,若![]() ,
,![]() ,求
,求![]() 边上的中线
边上的中线![]() 的取值范围.小明在组内经过合作交流,得到了如下的解决方法:将
的取值范围.小明在组内经过合作交流,得到了如下的解决方法:将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,把
,把![]() 、
、![]() 、
、![]() 集中在
集中在![]() 中,利用三角形的三边关系可得
中,利用三角形的三边关系可得![]() ,则
,则![]() ;
;
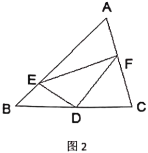
(2)问题解决:受到(1)的启发,请你证明下面命题:如图2,在![]() 中,
中,![]() 是
是![]() 边上的中点,
边上的中点,![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
①求证:![]() ;
;
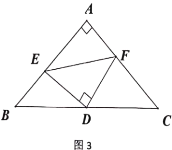
②如图3,若![]() ,探索线段
,探索线段![]() 、
、![]() 、
、![]() 之间的等量关系,并加以证明.
之间的等量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
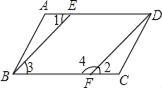
【题目】如图,已知AD∥BC,∠3+∠4=180°,要证∠1=∠2,请完善证明过程,并在括号内填上相应依据:
∵AD∥BC(已知)
∴∠l=∠3( ),
∵∠3+∠4=180°(已知),
∴BE∥DF( ),
∴ = ( ).
∴∠1=∠2( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 点
点![]() 在边
在边![]() 上,
上,![]() 点
点![]() 为边
为边![]() 上一动点,连接
上一动点,连接![]() 与
与![]() 关于
关于![]() 所在直线对称,点
所在直线对称,点![]() 分别为
分别为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 所在直线于点
所在直线于点![]() ,连接
,连接![]() .当
.当![]() 为直角三角形时,
为直角三角形时,![]() 的长为_________ .
的长为_________ .
查看答案和解析>>
科目:初中数学 来源: 题型:
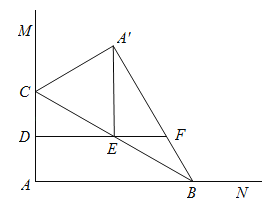
【题目】已知:∠MON=36°,OE平分∠MON,点A,B分别是射线OM,OE,上的动点(A,B不与点O重合),点D是线段OB上的动点,连接AD并延长交射线ON于点C,设∠OAC=x,
(1)如图1,若AB∥ON,则
①∠ABO的度数是______;
②当∠BAD=∠ABD时,x=______;
当∠BAD=∠BDA时,x=______;
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ABD中有两个相等的角?若存在,求出x的值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com