
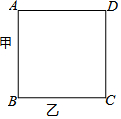
 如图,某人沿着边长为90米的正方形,按A→C→D→B→A…方向运动,甲从A以64米/分的速度,乙从C以90米/分的速度行走,当乙第一次追上甲时在正方形的( )
如图,某人沿着边长为90米的正方形,按A→C→D→B→A…方向运动,甲从A以64米/分的速度,乙从C以90米/分的速度行走,当乙第一次追上甲时在正方形的( )| A. | AB边上 | B. | CA边上 | C. | DC边上 | D. | BD边上 |
分析 设经过x分乙第一次追上甲,根据甲、乙速度差×时间=二者之间的距离即可得出关于x的一元一次方程,解之即可得出x值,再根据路程=速度×时间结合运动路径即可得出当乙第一次追上甲时在正方形的BD边上.
解答 解:设经过x分乙第一次追上甲,
根据题意得:(90-64)x=90+90$\sqrt{2}$+90,
解得:x=$\frac{90+45\sqrt{2}}{13}$,
∴64x=64×$\frac{90+45\sqrt{2}}{13}$≈756.33.
∵90$\sqrt{2}$+90+90$\sqrt{2}$+90+90$\sqrt{2}$+90≈651.78<756.33<779.04≈90$\sqrt{2}$+90+90$\sqrt{2}$+90+90$\sqrt{2}$+90+90$\sqrt{2}$,
∴当乙第一次追上甲时在正方形的BD边上.
故选D.
点评 本题考查了一元一次方程的应用,根据甲、乙速度差×时间=二者之间的距离列出关于x的一元一次方程是解题的关键.


科目:初中数学 来源: 题型:解答题
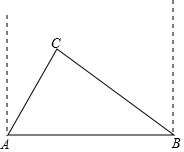 某县城在进行城市规划建设中,准备在相距1.6千米的两个超市A、B之间,扩建街道的宽度,但在A地的北偏东30°,B地的北偏西60°的C处有一半径为0.5千米的住宅小区,问在扩建公路时,这个小区是否有居民需要搬迁?($\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
某县城在进行城市规划建设中,准备在相距1.6千米的两个超市A、B之间,扩建街道的宽度,但在A地的北偏东30°,B地的北偏西60°的C处有一半径为0.5千米的住宅小区,问在扩建公路时,这个小区是否有居民需要搬迁?($\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1,2 | B. | 2,3 | C. | $\frac{1}{2}$,5 | D. | $\frac{1}{2}$,2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6元 | B. | 6x元 | C. | (1.4x+2.8)元 | D. | 1.4x元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com