
分析 首先找到驻点,确定x的取值范围,分类讨论确定n和m的值,再计算-nm的值.
解答 解:因为|x+1|≥0,|x-1|≥0
当|x+1|=0时,x=-1;当|x-1|=0时,x=1.
当x=1或-1时,n=|x+1|+|x-1|=2.
因为当x≤-1时,|-x-1|-|x-1|=-x-1-(1-x)=-2;
当-1<x<1时,|-x-1|-|x-1|=x+1-(1-x)=2x,-2<2x<2;
当x≥1时,|-x-1|-|x-1|=x+1-(x-1)=2.
所以m=|-x-1|-|x-1|=2
所以-nm=-22=-4.
故答案为:-4.
点评 本题考查了绝对值的化简.运用分类讨论是解决本题的关键.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
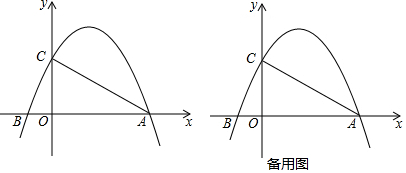
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
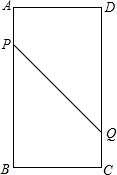 如图,在矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB以3cm/s的速度向点B移动,一直到达点B为止;同时,点Q从点C出发沿CD以2cm/s的速度向点D移动.设运动的时间为t.
如图,在矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB以3cm/s的速度向点B移动,一直到达点B为止;同时,点Q从点C出发沿CD以2cm/s的速度向点D移动.设运动的时间为t.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $2<\sqrt{5}<\root{3}{7}$ | B. | $2<\root{3}{7}<\sqrt{5}$ | C. | $\root{3}{7}<2<\sqrt{5}$ | D. | $\sqrt{5}<\root{3}{7}<2$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
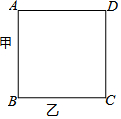 如图,某人沿着边长为90米的正方形,按A→C→D→B→A…方向运动,甲从A以64米/分的速度,乙从C以90米/分的速度行走,当乙第一次追上甲时在正方形的( )
如图,某人沿着边长为90米的正方形,按A→C→D→B→A…方向运动,甲从A以64米/分的速度,乙从C以90米/分的速度行走,当乙第一次追上甲时在正方形的( )| A. | AB边上 | B. | CA边上 | C. | DC边上 | D. | BD边上 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com