
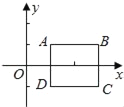
【题目】如图,点A(1,1),B(3,1),C(3,﹣1),D(1,﹣1)构成正方形ABCD,以AB为边做等边△ABE,则∠ADE和点E的坐标分别为( )
A. 15°和(2,1+![]() )
)
B. 75°和(2,![]() ﹣1)
﹣1)
C. 15°和(2,1+![]() )或75°和(2,
)或75°和(2,![]() ﹣1)
﹣1)
D. 15°和(2,1+![]() )或75°和(2,1﹣
)或75°和(2,1﹣![]() )
)
【答案】D
【解析】
分为两种情况:①当△ABE在正方形ABCD外时,过E作EM⊥AB于M,根据
等边三角形性质求出AM、AE,根据勾股定理求出EM,即可得出E的坐标,求出∠EAD,
根据三角形的内角和定理和等腰三角形性质即可求出∠ADE;②当等边△ABE在正方形
ABCD内时,同法求出此时E的坐标,求出∠DAE,根据三角形的内角和定理和等腰三角
形性质即可求出∠ADE.
分为两种情况:①△ABE在正方形ABCD外时,如图,过E作EM⊥AB于M,

∵等边三角形ABE,
∴AE=AB=3﹣1=2,
∴AM=1,
由勾股定理得:AE2=AM2+EM2,
∴22=12+EM2,
∴![]()
∵A(1,1),
∴E的坐标是![]()
∵等边△ABE和正方形ABCD,
∴∠DAB=90°,∠EAB=60°,AD=AE,
∴![]()
②同理当△ABE在正方形ABCD内时,同法求出E的坐标是![]()
∵∠DAE=90°﹣60°=30°,
AD=AE,
∴![]()
∴∠ADE和点E的坐标分别为15°,![]() 或75°,
或75°,![]()
故选:D.


科目:初中数学 来源: 题型:
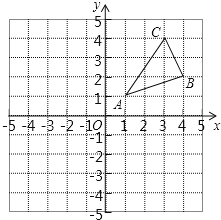
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC关于原点对称的△A1B1C1;
(2)四边形CBC1B1为 四边形;
(3)点P为平面内一点,若以点A、B、C、P为顶点的四边形为平行四边形,请直接写出所有满足条件的点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某经销商经销的冰箱二月份的售价比一月份每台降价500元,已知卖出相同数量的冰箱一月份的销售额为9万元,二月份的销售额只有8万元.
(1)二月份冰箱每台售价为多少元?
(2)为了提高利润,该经销商计划三月份再购进洗衣机进行销售,已知洗衣机每台进价为4000元,冰箱每台进价为3500元,预计用不多于7.6万元的资金购进这两种家电共20台,设冰箱为y台(y≤12),请问有几种进货方案?
(3)三月份为了促销,该经销商决定在二月份售价的基础上,每售出一台冰箱再返还顾客现金a元,而洗衣机按每台4400元销售,这种情况下,若(2)中各方案获得的利润相同,则a应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
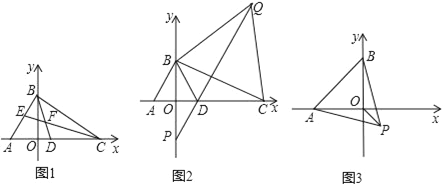
【题目】如图,在平面直角坐标系中,A(﹣3,0),点 B是 y轴正半轴上一动点,点C、D在 x正半轴上.
(1)如图,若∠BAO=60°,∠BCO=40°,BD、CE 是△ABC的两条角平分线,且BD、CE交于点F,直接写出CF的长_____.
(2)如图,△ABD是等边三角形,以线段BC为边在第一象限内作等边△BCQ,连接 QD并延长,交 y轴于点 P,当点 C运动到什么位置时,满足 PD=![]() DC?请求出点C的坐标;
DC?请求出点C的坐标;
(3)如图,以AB为边在AB的下方作等边△ABP,点B在 y轴上运动时,求OP的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郑州市自2019年12月1日起推行垃圾分类,广大市民对垃圾桶的需求剧增.为满足市场需求,某超市花了7900元购进大小不同的两种垃圾桶共800个,其中,大桶和小桶的进价及售价如表所示.
大桶 | 小桶 | |
进价(元/个) | 18 | 5 |
售价(元/个) | 20 | 8 |
(1)该超市购进大桶和小桶各多少个?
(2)当小桶售出了300个后,商家决定将剩下的小桶的售价降低1元销售,并把其中一定数量的小桶作为赠品,在顾客购买大桶时,买一赠一(买一个大桶送一个小桶),送完即止.
请问:超市要使这批垃圾桶售完后获得的利润为1550元,那么小桶作为赠品送出多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(-3,3),B(-4,-2),C(-1,-1).
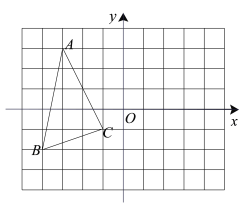
(1)在图中作出△ABC关于y轴对称的△A'B'C',并写出点C'的坐标________;
(2)在y轴上画出点P,使PA+PC最小,并直接写出P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,射线CM⊥BC,且BC=4,AB=1,点P是线段BC(不与点B、C重合)上的动点,过点P作DP⊥AP交射线CM于点D,连结AD.

(1)如图1,若BP=3,求△ABP的周长;
(2)如图2,若DP平分∠ADC,试猜测PB和PC的数量关系,并说明理由;
(3)若△PDC是等腰三角形,作点B关于AP的对称点B′,连结B′D,则B′D=_____.(请直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y=的第一象限的那一支上,AB垂直于x轴与点B,
点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE
的面积为3,则k的值为 ▲ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车开往距离出发地![]() 的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前
的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前![]() 到达目的地,设前一个小时的行驶速度为
到达目的地,设前一个小时的行驶速度为![]()
(1)直接用![]() 的式子表示提速后走完剩余路程的时间为
的式子表示提速后走完剩余路程的时间为
(2)求汽车实际走完全程所花的时间.
(3)若汽车按原路返回,司机准备一半路程以![]() 的速度行驶,另一半路程以
的速度行驶,另一半路程以![]() 的速度行驶(
的速度行驶(![]() ),朋友提醒他一半时间以
),朋友提醒他一半时间以![]() 的速度行驶,另一半时间以
的速度行驶,另一半时间以![]() 的速度行驶更快,你觉得谁的方案更快?请说明理由.
的速度行驶更快,你觉得谁的方案更快?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com