
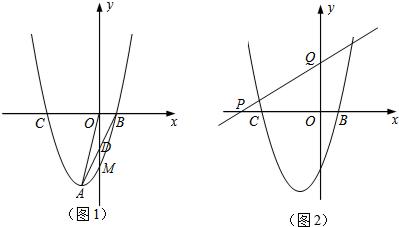
分析 (1)作AH⊥BC于H,利用三角形的相似求出点B的坐标,进而求出a的值;
(2)设N(a,a2+2a-3),yCM=-x-3,求出△CNM的面积最大值,即可求出四边形CBMN的面积最大值;
(3)分两种情况进行讨论:①直线l和直线m垂直,根据两直线关系求出直线m的解析式;②当直线m的斜率大于直线l的斜率时,画出图形,利用三角形相似的性质解答,求出直线m的斜率k即可.
解答 解:(1)A(-1,-4)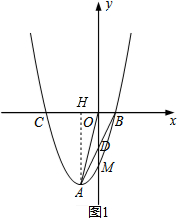 ,
,
作AH⊥BC于H,如图1,
∵OD恰好平分△OAB的面积,
∴BD:AB=1:2,
由△DOB∽△AHB,
得BO:BH=BD:AB=1:2,
∴B(1,0),
则解析式为y=x2+2x-3;
(2)M(0,-3)
设N(a,a2+2a-3),yCM=-x-3,
S△CMN=$\frac{1}{2}$[(-a-3)-(a2+2a-3)]×3=-$\frac{3}{2}$(a+$\frac{3}{2}$)2+$\frac{27}{8}$
当△CNM的面积最大时,四边形CBMN的面积最大.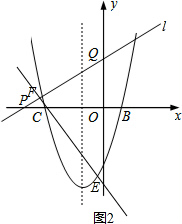 则N(-$\frac{3}{2}$,-$\frac{15}{4}$);
则N(-$\frac{3}{2}$,-$\frac{15}{4}$);
(3)设直线PQ的解析式为y=mx+n,
∵点P(-4,0),Q(0,2),
∴$\left\{\begin{array}{l}{-4m+n=0}\\{n=2}\end{array}\right.$,
∴m=$\frac{1}{2}$,n=2,
∴y=$\frac{1}{2}$x+2,
设直线m的解析式为y=k(x+3),
如图2,
设直线m和l相交于点F,
当l和m垂直时,△PFC和△EFQ相似,
则直线m的斜率为-2,
则直线m的解析式为y=-2x-6;
如图3,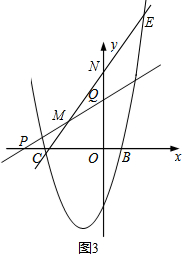
设直线m和l的交点为M,直线m与y轴的交点为N,k>$\frac{1}{2}$,
联立$\left\{\begin{array}{l}{y=\frac{1}{2}x+2}\\{y=k(x+3)}\end{array}\right.$,
解得x=$\frac{4-6k}{2k-1}$,y=$\frac{k}{2k-1}$,
则点M的坐标为($\frac{4-6k}{2k-1}$,$\frac{k}{2k-1}$),
若△PMC∽△NMQ,
则$\frac{3k-2}{1}=\frac{\frac{6k-4}{2k-1}}{\frac{k}{2k-1}}$,
解得k=2,
故直线m的解析式为y=2x+6.
综上所述直线m的解析式为y=-2x-6或y=2x+6.
点评 本题主要考查了二次函数综合题,此题涉及到待定系数法求函数解析式、相似三角形的判定与性质、求两直线的交点坐标等知识,解答(2)问的关键是求出△CMN的面积最大值,解答(3)问的关键是正确地作出图形,利用三角形相似定理进行解答,此题有一定的难度.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
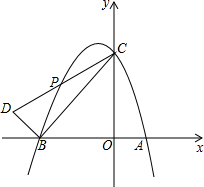 如图,抛物线y=-$\frac{1}{2}$x2+bx+4与x轴交于A(2,0)、B两点,与y轴交于点C.
如图,抛物线y=-$\frac{1}{2}$x2+bx+4与x轴交于A(2,0)、B两点,与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
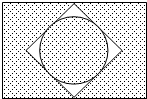 如图是“温州南”动车站前广场设计方案之一,其中大广场地面长方形的长200米,宽100米,大广场“含”一个边长为80米正方形广场,正方形广场又“含”一个半径为40米的圆形中心广场,按设计,图中阴影处铺设某种广场地砖.则广场地砖需要铺多少平方米?(π取3,结果精确到千位)
如图是“温州南”动车站前广场设计方案之一,其中大广场地面长方形的长200米,宽100米,大广场“含”一个边长为80米正方形广场,正方形广场又“含”一个半径为40米的圆形中心广场,按设计,图中阴影处铺设某种广场地砖.则广场地砖需要铺多少平方米?(π取3,结果精确到千位)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com