
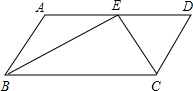
 如图,在?ABCD中,BE、CE分别平分∠ABC和∠BCD,且BE与CE相交于AD上同一点,若BE=12cm,CE=5cm.
如图,在?ABCD中,BE、CE分别平分∠ABC和∠BCD,且BE与CE相交于AD上同一点,若BE=12cm,CE=5cm.分析 (1)根据在?ABCD中,BE、CE分别平分∠ABC和∠BCD,可以得到∠BEC的度数,从而可以判断△BCE的形状,根据BE=12cm,CE=5cm,可以求得BC的长;
(2)根据?ABCD中,BE、CE分别平分∠ABC和∠BCD,进行合理的转化,从而可以证明结论成立;
(3)根据题意和(1)(2)小题的结果,可以得到AB的长;
(4)由题意可以求得?ABCD的周长,要求?ABCD的面积只要求出△BEC的面积即可,如果以BC做底边则△BEC和?ABCD是同底等高的,由BE=12cm,CE=5cm,∠BEC=90°,从而可以解答本题.
解答 解:(1)△BCE是直角三角形,
理由:∵在?ABCD中,BE、CE分别平分∠ABC和∠BCD,
∴∠ABC+∠BCD=180°,∠ABE=∠EBC,∠BCE=∠ECD,
∴∠EBC+∠ECB=90°,
∴∠BEC=90°,
∴△BCE是直角三角形;
∵∠BEC=90°,BE=12cm,CE=5cm,
∴BC=$\sqrt{B{E}^{2}+C{E}^{2}}=\sqrt{1{2}^{2}+{5}^{2}}=13$cm;
(2)证明:∵在?ABCD中,BE、CE分别平分∠ABC和∠BCD,
∴AB=CD,AD∥BC,∠ABE=∠EBC,∠BCE=∠ECD,
∴∠AEB=∠EBC,∠BCE=∠CED,
∴∠ABE=∠AEB,∠CED=∠ECD,
∴AB=AE,DE=DC,
∵AB=DC,
∴AE=DE,
∴点E是AD的中点;
(3)∵在?ABCD中,点E为CD的中点,BC=13cm,
∴AD=BC=13cm,
由(2)知,AB=$\frac{1}{2}$AD,
∴AB=6.5cm;
(4)∵在?ABCD中,AB=CD=6.5cm,AD=BC=13cm,
∴?ABCD的周长是:6.5+13+6.5+13=39cm,
∵△BEC是直角三角形,BE=12cm,CE=5cm,∠BEC=90°,
∴△BEC的面积是:12×5÷2=30cm2,
∴?ABCD的面积是:2×30=60cm2.
点评 本题考查四边形综合题,解题的关键是明确题意,找出所求问题需要的条件,利用勾股定理和数形结合的思想解答问题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 该调查方式为普查 | B. | 调查可用画正字的方式统计人数 | ||
| C. | 该调查可采用问卷调查 | D. | 该调查的样本容量为200 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com