
【题目】已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD. 
(1)求证:∠DAC=∠DBA;
(2)求证:P是线段AF的中点;
(3)连接CD,若CD﹦3,BD﹦4,求⊙O的半径和DE的长.
【答案】
(1)证明:∵BD平分∠CBA,
∴∠CBD=∠DBA,
∵∠DAC与∠CBD都是弧CD所对的圆周角,
∴∠DAC=∠CBD,
∴∠DAC=∠DBA;
(2)证明:∵AB为直径,
∴∠ADB=90°,
∵DE⊥AB于E,
∴∠DEB=90°,
∴∠1+∠3=∠5+∠3=90°,
∴∠1=∠5=∠2,
∴PD=PA,
∵∠4+∠2=∠1+∠3=90°,且∠ADB=90°,
∴∠3=∠4,
∴PD=PF,
∴PA=PF,即P是线段AF的中点;
(3)解:连接CD,
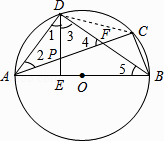
∵∠CBD=∠DBA,
∴CD=AD,
∵CD﹦3,∴AD=3,
∵∠ADB=90°,
∴AB=5,
故⊙O的半径为2.5,
∵DE×AB=AD×BD,
∴5DE=3×4,
∴DE=2.4.
即DE的长为2.4.
【解析】(1)利用角平分线的性质得出∠CBD=∠DBA,进而得出∠DAC=∠DBA;(2)利用圆周角定理得出∠ADB=90°,进而求出∠PDF=∠PFD,则PD=PF,求出PA=PF,即可得出答案;(3)利用勾股定理得出AB的长,再利用三角形面积求出DE即可.


 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】周末,小明骑自行车从家里出发到野外郊游.从家出发1小时后到达南亚所(景点),游玩一段时间后按原速前往湖光岩.小明离家1小时50分钟后,妈妈驾车沿相同路线前往湖光岩,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象. 
(1)求小明骑车的速度和在南亚所游玩的时间;
(2)若妈妈在出发后25分钟时,刚好在湖光岩门口追上小明,求妈妈驾车的速度及CD所在直线的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,已知AD∥BC,AB=DC,AC与BD交于点O,延长BC到E,使得CE=AD,连接DE. 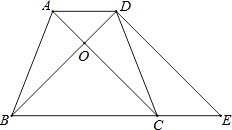
(1)求证:BD=DE.
(2)若AC⊥BD,AD=3,SABCD=16,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在信宜市某“三华李”种植基地有A、B两个品种的树苗出售,已知A种比B种每株多2元,买1株A种树苗和2株B种树苗共需20元.
(1)问A、B两种树苗每株分别是多少元?
(2)为扩大种植,某农户准备购买A、B两种树苗共360株,且A种树苗数量不少于B种数量的一半,请求出费用最省的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后,得到△A′O′B,且反比例函数y= ![]() 的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k= .
的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k= . 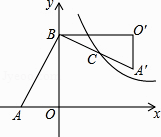
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y= ![]() 在第一象限的图象经过点B.若OA2﹣AB2=12,则k的值为 .
在第一象限的图象经过点B.若OA2﹣AB2=12,则k的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:点A(x,y)为平面直角坐标系内的点,若满足x=y,则把点A 叫做“平衡点”.例如:M(1,1),N(﹣2,-2)都是“平衡点”.当﹣1≤x≤3 时,直线y=2x+m 上有“平衡点”,则m 的取值范围是( )
A.0≤m≤1
B.﹣1≤m≤0
C.﹣3≤m≤3
D.﹣3≤m≤1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+(2k﹣1)x+k2﹣1=0有两个实数根x1 , x2 .
(1)求实数k的取值范围;
(2)若x1 , x2满足x12+x22=16+x1x2 , 求实数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的统计图反映了我国与“一带一路”沿线部分地区的贸易情况. 2011﹣2016年我国与东南亚地区和东欧地区的贸易额统计图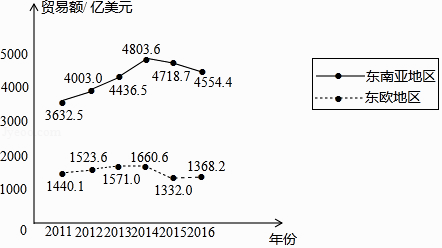
(以上数据摘自《“一带一路”贸易合作大数据报告(2017)》)
根据统计图提供的信息,下列推理不合理的是( )
A.与2015年相比,2016年我国与东欧地区的贸易额有所增长
B.2011﹣2016年,我国与东南亚地区的贸易额逐年增长
C.2011﹣2016年,我国与东南亚地区的贸易额的平均值超过4200亿美元
D.2016年我国与东南亚地区的贸易额比我国与东欧地区的贸易额的3倍还多
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com