
【题目】如图,在Rt△AOB中,直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后,得到△A′O′B,且反比例函数y= ![]() 的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k= .
的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k= . 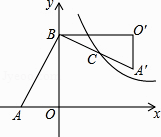
【答案】6
【解析】解:设点C坐标为(x,y),作CD⊥BO′交边BO′于点D,
∵tan∠BAO=2,
∴ ![]() =2,
=2,
∵S△ABO= ![]() AOBO=4,
AOBO=4,
∴AO=2,BO=4,
∵△ABO≌△A'O'B,
∴AO=A′O′=2,BO=BO′=4,
∵点C为斜边A′B的中点,CD⊥BO′,
∴CD= ![]() A′O′=1,BD=
A′O′=1,BD= ![]() BO′=2,
BO′=2,
∴x=BO﹣CD=4﹣1=3,y=BD=2,
∴k=xy=32=6.
所以答案是6.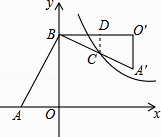
【考点精析】利用反比例函数的图象和旋转的性质对题目进行判断即可得到答案,需要熟知反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.


 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:
【题目】把大小和形状完全相同的6张卡片分成两组,每组3张,分别标上1、2、3,将这两组卡片分别放入两个盒子中搅匀,再从中随机抽取一张.
(1)试求取出的两张卡片数字之和为奇数的概率;
(2)若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,过点A(0,4)的圆的圆心坐标为C(2,0),B是第一象限圆弧上的一点,且BC⊥AC,抛物线y= ![]() x2+bx+c经过C、B两点,与x轴的另一交点为D.
x2+bx+c经过C、B两点,与x轴的另一交点为D.
(1)点B的坐标为( , ),抛物线的表达式为;
(2)如图2,求证:BD∥AC;
(3)如图3,点Q为线段BC上一点,且AQ=5,直线AQ交⊙C于点P,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与x轴交于点A和点B,与y轴交于点C,已知点B的坐标为(3,0).
与x轴交于点A和点B,与y轴交于点C,已知点B的坐标为(3,0).
(1)求a的值和抛物线的顶点坐标;
(2)分别连接AC、BC.在x轴下方的抛物线上求一点M,使△AMC与△ABC的面积相等;
(3)设N是抛物线对称轴上的一个动点,d=|AN﹣CN|.探究:是否存在一点N,使d的值最大?若存在,请直接写出点N的坐标和d的最大值;若不存在,请简单说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与x轴交于点A和点B,与y轴交于点C,已知点B的坐标为(3,0).
与x轴交于点A和点B,与y轴交于点C,已知点B的坐标为(3,0).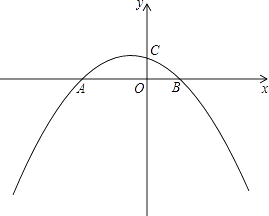
(1)求a的值和抛物线的顶点坐标;
(2)分别连接AC、BC.在x轴下方的抛物线上求一点M,使△AMC与△ABC的面积相等;
(3)设N是抛物线对称轴上的一个动点,d=|AN﹣CN|.探究:是否存在一点N,使d的值最大?若存在,请直接写出点N的坐标和d的最大值;若不存在,请简单说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD. 
(1)求证:∠DAC=∠DBA;
(2)求证:P是线段AF的中点;
(3)连接CD,若CD﹦3,BD﹦4,求⊙O的半径和DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学生社团为了解本校学生喜欢球类运动的情况,随机抽取了若干名学生进行问卷调查,要求每位学生只能填写一种自己喜欢的球类运动,并将调查的结果绘制成如下的两幅不完整的统计图. 
请根据统计图表提供的信息,解答下列问题:
(1)参加调查的人数共有人;在扇形图中,m=;将条形图补充完整;
(2)如果该校有3500名学生,则估计喜欢“篮球”的学生共有多少人?
(3)该社团计划从篮球、足球和乒乓球中,随机抽取两种球类组织比赛,请用树状图或列表法,求抽取到的两种球类恰好是“篮球”和“足球”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,10个不同的正偶数按下图排列,箭头上方的每个数都等于其下方两数的和,如 ![]() ,表示a1=a2+a3 , 则a1的最小值为( )
,表示a1=a2+a3 , 则a1的最小值为( ) 
A.32
B.36
C.38
D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节当天,小明带了四个粽子(除味道不同外,其它均相同),其中两个是大枣味的,另外两个是火腿味的,准备按数量平均分给小红和小刚两个好朋友.
(1)请你用树状图或列表的方法表示小红拿到的两个粽子的所有可能性.
(2)请你计算小红拿到的两个粽子刚好是同一味道的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com