
【题目】在平面直角坐标系中,抛物线y=ax2﹣2ax﹣3与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,顶点为D,且过点(2,﹣3a).
(1)求抛物线的解析式;
(2)抛物线上是否存在一点P,过点P作PM⊥BD,垂足为点M,PM=2DM?若存在,求点P的坐标;若不存在,说明理由.
(3)在(2)的条件下,求△PMD的面积.
【答案】(1)(1,﹣4);(2)存在,(﹣![]() ,﹣
,﹣![]() );(3)
);(3)![]() .
.
【解析】
(1)将点的坐标(2,﹣3a)代入抛物线表达式得:﹣3a=4a﹣4a﹣3,即可求解;
(2)利用△PGM∽△MHD,得![]() =2,分别求出线段长度即可求解;
=2,分别求出线段长度即可求解;
(3)利用S=![]() PMDM,即可求解.
PMDM,即可求解.
(1)将点的坐标(2,﹣3a)代入抛物线表达式得:﹣3a=4a﹣4a﹣3,解得:a=1,
故抛物线的表达式为:y=x2﹣2x﹣3,
令y=0,解得:x=3或﹣1,
即点A、B的坐标分别为(﹣1,0)、(3,0),
函数对称轴为x=1,则点D的坐标为(1,﹣4);
(2)存在.理由:
将点B、D的坐标代入一次函数表达式:y=kx+b得:
![]() ,解得:
,解得:![]() ,
,
即:直线BD的表达式为:y=2x﹣6,
过点M作GH∥y轴,分别过点P、点D作x轴的平行线交于点G、H,

∵∠PMG+∠DMH=90°,∠DMH+∠MDH=90°,
∴∠PMG=∠MDH,
∠PGM=∠MHD=90°,
∴△PGM∽△MHD,
∴![]() =2,
=2,
设点M、P的横坐标分别为m,n,则其坐标分别为(m,2m﹣6)、(n,n2﹣2n﹣3),
则:PG=m﹣n,MH=2m﹣6﹣(﹣4)=2m﹣2,
即:m﹣n=4m﹣4…①,
GM=n2﹣2n﹣3﹣2m+6=n2﹣2n﹣2m+3,DH=m﹣1,
即:n2﹣2n﹣2m+3=2m﹣2…②
①②联立并解得:n=1或﹣![]() (n=1不合题意,舍去),
(n=1不合题意,舍去),
则n=﹣![]() ,m=
,m=![]() ,点M坐标为(
,点M坐标为(![]() ,﹣
,﹣![]() ),
),
故点P的坐标为(﹣![]() ,﹣
,﹣![]() );
);
(3)由勾股定理得:
PM=![]() ,
,
DM=![]() ,
,
S=![]() PMDM=
PMDM=![]() .
.


 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于点E、F、G,过点D作⊙O的切线交BC于点M,切点为N,则DM的长为( )
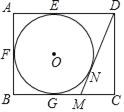
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求化简:(a﹣1)÷![]() ,并选择你喜欢的整数a,b代入求值.
,并选择你喜欢的整数a,b代入求值.
小聪计算这一题的过程如下:
解:原式=(a﹣1)÷![]() …①
…①
=(a﹣1)![]() …②
…②
=![]() …③
…③
当a=1,b=1时,原式=![]() …④
…④
以上过程有两处关键性错误,第一次出错在第_____步(填序号),原因:_____;
还有第_____步出错(填序号),原因:_____.
请你写出此题的正确解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形 ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.

(1)求AO的长;
(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=![]() AM;
AM;
(3)连接EM,若△AEM的面积为40,请直接写出△AFM的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
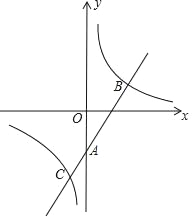
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与y轴相交于点A,与反比例函数y2=![]() (k≠0)的图象相交于点B(3,2)、C(﹣1,n).
(k≠0)的图象相交于点B(3,2)、C(﹣1,n).
(1)求一次函数和反比例函数的解析式;
(2)根据图象,直接写出y1>y2时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线C1:y=ax2﹣2ax+c(a<0)与x轴交于A、B两点,与y轴交于点C.已知点A的坐标为(﹣1,0),点O为坐标原点,OC=3OA,抛物线C1的顶点为G.

(1)求出抛物线C1的解析式,并写出点G的坐标;
(2)如图2,将抛物线C1向下平移k(k>0)个单位,得到抛物线C2,设C2与x轴的交点为A′、B′,顶点为G′,当△A′B′G′是等边三角形时,求k的值:
(3)在(2)的条件下,如图3,设点M为x轴正半轴上一动点,过点M作x轴的垂线分别交抛物线C1、C2于P、Q两点,试探究在直线y=﹣1上是否存在点N,使得以P、Q、N为顶点的三角形与△AOQ全等,若存在,直接写出点M,N的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
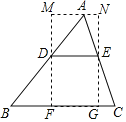
【题目】如图,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线.过点D、E作DF∥EG,分别交BC于F、G,沿DF将△BDF剪下,并顺时针旋转180°与△AMD重叠,沿EG将△CEG剪下,并逆时针旋转180°与△ANE重叠,则四边形MFGN周长的最小值是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读对话,解答问题:
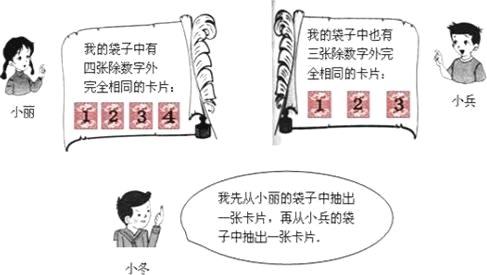
(1)分别用a、b表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字,请用树状图法或列表法写出(a,b)的所有取值;
(2)求在(a,b)中使关于x的一元二次方程x2﹣ax+2b=0有实数根的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的身体素质,教育行政部门规定每位学生每天参加户外活动的平均时间不少于1小时. 为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,
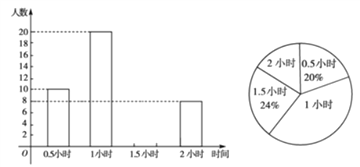
请你根据图中提供的信息解答下列问题:
(1)在这次调查中共调查了多少名学生?
(2)求户外活动时间为1.5小时的人数,并补充频数分布直方图;
(3)户外活动时间的众数和中位数分别是多少?
(4)若该市共有20000名学生,大约有多少学生户外活动的平均时间符合要求?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com