
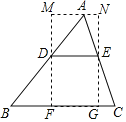
【题目】如图,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线.过点D、E作DF∥EG,分别交BC于F、G,沿DF将△BDF剪下,并顺时针旋转180°与△AMD重叠,沿EG将△CEG剪下,并逆时针旋转180°与△ANE重叠,则四边形MFGN周长的最小值是__.
【答案】10![]() +8.
+8.
【解析】
先判断出四边形MFGN是平行四边形,再判断出MN=FG=DE=4,进而判断出MF⊥BC时,四边形MFGN的周长最小,最后构造出直角三角形求出AH即可得出结论.
如图,

∵MN∥BC,FM∥GN,
∴四边形MFGN是平行四边形,
∴MF=NG,MN=FG,
∵DE是△ABC的中位线,
∴DE=![]() BC=4,DE∥BC,
BC=4,DE∥BC,
∴MN=FG=![]() BC=4,
BC=4,
∴四边形MFGN周长=2(MF+FG)=2MF+8,
∴MF⊥BC时,MF最短,
即:四边形MFGN的周长最小,
过点A作AH⊥BC于H,
∴FM=AH
在Rt△ABH中,∠B=45°,AB=10,
∴AH=![]() ,
,
∴四边形MFGN的周长最小为2MF+8=10![]() +8.
+8.
故答案为10![]() +8.
+8.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,AD是高,E、F分别是AB、AC的中点,
中,AD是高,E、F分别是AB、AC的中点,
(1)AB=10,AC=8,求四边形AEDF的周长;
(2)EF与AD有怎样的位置关系,证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的序号____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=ax2﹣2ax﹣3与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,顶点为D,且过点(2,﹣3a).
(1)求抛物线的解析式;
(2)抛物线上是否存在一点P,过点P作PM⊥BD,垂足为点M,PM=2DM?若存在,求点P的坐标;若不存在,说明理由.
(3)在(2)的条件下,求△PMD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我国海监船在钓鱼岛附近的O处观测到一可疑船正匀速直线航行我国海域,当该可疑船位于点O的北偏东30°方向上的点A处(OA=20![]() km)时,我方开始向对方喊话,但该可疑船仍匀速航行,40min后,又测得该可疑船位于点O的正北方向上的点B处,且OB=20km,求该可疑船航行的速度.
km)时,我方开始向对方喊话,但该可疑船仍匀速航行,40min后,又测得该可疑船位于点O的正北方向上的点B处,且OB=20km,求该可疑船航行的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦期间,某宾馆有50个房间供游客居住,当每个房间每天的定价为180元时,房间会全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用.
(1)若房价定为200元时,求宾馆每天的利润;
(2)房价定为多少时,宾馆每天的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市移动通讯公司开设了两种通讯业务: “全球通” 使用者先缴50元月基础费, 然后每通话1分钟, 再付电话费0.4元; “神州行” 不缴月基础费, 每通话1分钟, 付话费0.6元(这里均指市内通话). 若一个月内通话x分钟, 两种通讯方式的费用分别为y1元和y2元.
(1)写出y1、y2与x之间的函数关系式;
(2)一个月内通话多少分钟, 两种通讯方式的费用相同?
(3)若某人预计一个月内使用话费200元, 则应选择哪种通讯方式较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
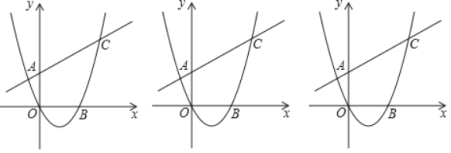
【题目】如图,二次函数y=ax2﹣4ax(a≠0)的图象与直线y=kx+3交于点A(﹣1,![]() )、点C两点.
)、点C两点.
(1)求a,k的值;
(2)点P在第一象限的抛物线上,其横坐标为t,连接PC、PA,设△PCA的面积为S,求S关于t的函数关系式:(直接写出t的取值范围)
(3)在(2)的条件下,作CE⊥x轴于E,点P直线y=kx+3下方时,连接OP、BC交于D,连接ED,当∠ODE=90°时,求t和S的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com