
°æƒø°ø“—÷™£∫‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨![]() Œ™
Œ™![]() ÷·∏∫∞Î÷·…œµƒµ„£¨
÷·∏∫∞Î÷·…œµƒµ„£¨![]() Œ™
Œ™![]() ÷·∏∫∞Î÷·…œµƒµ„.
÷·∏∫∞Î÷·…œµƒµ„.
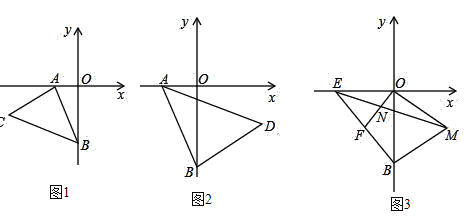
(1)»ÁÕº1£¨“‘![]() µ„Œ™∂•µ„°¢
µ„Œ™∂•µ„°¢![]() Œ™—¸‘⁄µ⁄»˝œÛœÞ◊˜µ»—¸
Œ™—¸‘⁄µ⁄»˝œÛœÞ◊˜µ»—¸![]() £¨»Ù
£¨»Ù![]() £¨
£¨![]() £¨ ‘«Û
£¨ ‘«Û![]() µ„µƒ◊¯±Í£ª
µ„µƒ◊¯±Í£ª
(2)»ÁÕº![]() £¨»Ùµ„
£¨»Ùµ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() £¨µ„
£¨µ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() £¨µ„
£¨µ„![]() µƒ◊ð◊¯±ÍŒ™
µƒ◊ð◊¯±ÍŒ™![]() £¨“‘
£¨“‘![]() Œ™∂•µ„£¨
Œ™∂•µ„£¨![]() Œ™—¸◊˜µ»—¸
Œ™—¸◊˜µ»—¸![]() . ‘Œ £∫µ±
. ‘Œ £∫µ±![]() µ„—ÿ
µ„—ÿ![]() ÷·∏∫∞Î÷·œÚœ¬‘À∂Ø«“∆‰À˚Ãıº˛∂º≤ª±‰ ±£¨’˚ Ω
÷·∏∫∞Î÷·œÚœ¬‘À∂Ø«“∆‰À˚Ãıº˛∂º≤ª±‰ ±£¨’˚ Ω![]() µƒ÷µ «∑Ò∑¢…˙±‰ªØ£ø»Ù≤ª∑¢…˙±‰ªØ£¨«Î«Û≥ˆ∆‰÷µ£ª»Ù∑¢…˙±‰ªØ£¨«ÎÀµ√˜¿Ì”…£ª
µƒ÷µ «∑Ò∑¢…˙±‰ªØ£ø»Ù≤ª∑¢…˙±‰ªØ£¨«Î«Û≥ˆ∆‰÷µ£ª»Ù∑¢…˙±‰ªØ£¨«ÎÀµ√˜¿Ì”…£ª
(3)»ÁÕº![]() £¨
£¨![]() Œ™
Œ™![]() ÷·∏∫∞Î÷·…œµƒ“ªµ„£¨«“
÷·∏∫∞Î÷·…œµƒ“ªµ„£¨«“![]() £¨
£¨![]() ”⁄µ„
”⁄µ„![]() £¨“‘
£¨“‘![]() Œ™±þ◊˜µ»±þ
Œ™±þ◊˜µ»±þ![]() £¨¡¨Ω”
£¨¡¨Ω”![]() Ωª
Ωª![]() ”⁄µ„
”⁄µ„![]() £¨ ‘ÃΩÀ˜£∫‘⁄œþ∂Œ
£¨ ‘ÃΩÀ˜£∫‘⁄œþ∂Œ![]() °¢
°¢![]() ∫Õ
∫Õ![]() ÷–£¨ƒƒÃıœþ∂Œµ»”⁄
÷–£¨ƒƒÃıœþ∂Œµ»”⁄![]() ”Î
”Î![]() µƒ≤Óµƒ“ª∞Σø«Îƒ„–¥≥ˆ’‚∏ˆµ»¡øπÿœµ£¨≤¢º”“‘÷§√˜.
µƒ≤Óµƒ“ª∞Σø«Îƒ„–¥≥ˆ’‚∏ˆµ»¡øπÿœµ£¨≤¢º”“‘÷§√˜.
°æ¥∞∏°ø(1) C(-6,-2);(2)≤ª∑¢…˙±‰ªØ£¨÷µŒ™![]() £ª£®3£©EN=
£ª£®3£©EN=![]() (EM-ON)£¨÷§√˜º˚œÍΩ‚.
(EM-ON)£¨÷§√˜º˚œÍΩ‚.
°æΩ‚Œˆ°ø
£®1£©◊˜CQ°ÕOA”⁄µ„Q,ø…“‘÷§√˜![]() £¨”…QC=AD,AQ=BO,‘Ÿ”…Ãıº˛æÕø…“‘«Û≥ˆµ„Cµƒ◊¯±Í£ª
£¨”…QC=AD,AQ=BO,‘Ÿ”…Ãıº˛æÕø…“‘«Û≥ˆµ„Cµƒ◊¯±Í£ª
£®2£©◊˜DP°ÕOB”⁄µ„P£¨ø…“‘÷§√˜![]() £¨‘Ú”–BP=OB-PO=m-(-n)=m+nŒ™∂®÷µ£¨¥”∂¯ø…“‘«Û≥ˆΩ·¬€
£¨‘Ú”–BP=OB-PO=m-(-n)=m+nŒ™∂®÷µ£¨¥”∂¯ø…“‘«Û≥ˆΩ·¬€![]() µƒ÷µ≤ª±‰Œ™
µƒ÷µ≤ª±‰Œ™![]() .
.
£®3£©◊˜BH°ÕEB”⁄µ„B£¨”…Ãıº˛ø…“‘µ√≥ˆ°œ1=30°„,°œ2=°œ3=°œEMO=15°„,°œEOF=°œBMG=45°„,EO=BM,ø…“‘÷§√˜![]() £¨‘ÚGM=ON,æÕ”–EM-ON=EM-GM=EG,◊Ó∫Û”…∆Ω––œþ∑÷œþ∂Œ≥…±»¿˝∂®¿ÌæÕø…µ√≥ˆEN=
£¨‘ÚGM=ON,æÕ”–EM-ON=EM-GM=EG,◊Ó∫Û”…∆Ω––œþ∑÷œþ∂Œ≥…±»¿˝∂®¿ÌæÕø…µ√≥ˆEN=![]() (EM-ON).
(EM-ON).
£®1£©»ÁÕº£®1£©◊˜CQ°ÕOA”⁄Q,
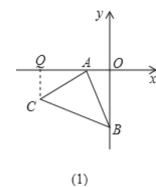
°ý°œAQC=90°„,
°þ![]() Œ™µ»—¸÷±Ω«»˝Ω«–Œ£¨
Œ™µ»—¸÷±Ω«»˝Ω«–Œ£¨
°ýAC=AB,°œCAB=90°„,
°ý°œQAC+°œOAB=90°„,
°þ°œQAC+°œACQ=90°„,
°ý°œACQ=°œBAO,
”÷°þAC=AB,°œAQC=°œAOB,
°ý![]() (AAS),
(AAS),
°ýCQ=AO,AQ=BO,
°þOA=2,OB=4,
°ýCQ=2,AQ=4,
°ýOQ=6,
°ýC(-6,-2).
(2)»ÁÕº£®2£©◊˜DP°ÕOB”⁄µ„P,
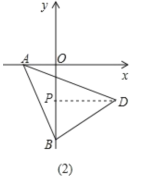
°ý°œBPD=90°„,
°þ![]() «µ»—¸÷±Ω«»˝Ω«–Œ£¨
«µ»—¸÷±Ω«»˝Ω«–Œ£¨
°ýAB=BD,°œABD=°œABO+°œOBD=90°„,
°þ°œOBD+°œBDP=90°„,
°ý°œABO=°œBDP,
”÷°þAB=BD,°œAOB=°œBPD=90°„,
°ý![]()
°ýAO=BP,
°þBP=OB-PO=m-(-n)=m+n,
°þA![]() ,
,
°ýOA=![]() ,
,
°ým+n=![]() ,
,
°ýµ±µ„B—ÿy÷·∏∫∞Î÷·œÚœ¬‘À∂Ø ±£¨AO=BP=m+n=![]() ,
,
°ý’˚ Ω![]() µƒ÷µ≤ª±‰Œ™
µƒ÷µ≤ª±‰Œ™![]() .
.
£®3£©![]()
÷§√˜£∫»ÁÕº£®3£©À˘ 棨‘⁄ME…œ»°“ªµ„G πµ√MG=ON,¡¨Ω”BG≤¢—”≥§£¨Ωªx÷·”⁄H.
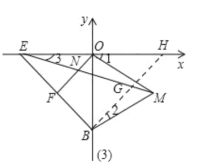
°þ![]() Œ™µ»±þ»˝Ω«–Œ£¨
Œ™µ»±þ»˝Ω«–Œ£¨
°ýBO=BM=MO,°œOBM=°œOMB=°œBOM=60°„,
°ýEO=MO,°œEBM=105°„,°œ1=30°„,
°þOE=OB,
°ýOE=OM=BM,
°ý°œ3=°œEMO=15°„,
°ý°œBEM=30°„,°œBME=45°„,
°þOF°ÕEB,
°ý°œEOF=°œBME,
°ý![]() ,
,
°ýBG=EN,
°þON=MG,
°ý°œ2=°œ3,
°ý°œ2=15°„,
°ý°œEBG=90°„,
°ýBG=![]() EG,
EG,
°ýEN=![]() EG,
EG,
°þEG=EM-GM,
°ýEN=![]() (EM-GM),
(EM-GM),
°ýEN=![]() (EM-ON).
(EM-ON).


 ø⁄À„Âø®º””¶”√ºؗµœµ¡–¥∞∏
ø⁄À„Âø®º””¶”√ºؗµœµ¡–¥∞∏ ◊€∫œ◊‘≤‚œµ¡–¥∞∏
◊€∫œ◊‘≤‚œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
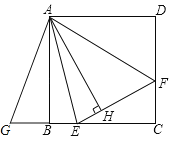
°æƒø°ø»ÁÕº£¨‘⁄’˝∑Ω–ŒABCDƒ⁄◊˜°œEAF=45°„£¨AEΩªBC”⁄µ„E£¨AFΩªCD”⁄µ„F£¨¡¨Ω”EF£¨π˝µ„A◊˜AH°ÕEF£¨¥π◊„Œ™H£¨Ω´°˜ADF»∆µ„AÀ≥ ±’Ζ˝◊™90°„µ√µΩ°˜ABG£¨»ÙBE=2£¨DF=3£¨‘ÚAHµƒ≥§Œ™______£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∂˛¥Œ∫Ø ˝y=ax2+bx+c(a°Ÿ0)µƒÕºœÛ»ÁÕºÀ˘ æ.”–œ¬¡–Ω·¬€:¢Ÿb2-4ac<0£ª¢⁄ab>0£ª¢€a-b+c=0£ª¢Ð4a+b=0£ª¢ðµ±y=2 ±£¨x÷ªƒÐµ»”⁄0.∆‰÷–’˝»∑µƒ «£® £©
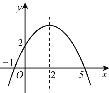
A. ¢Ÿ¢Ð B. ¢€¢Ð C. ¢⁄¢ð D. ¢€¢ð
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
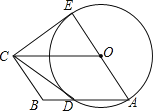
°æƒø°ø»ÁÕº£¨Àƒ±þ–ŒOABC «∆Ω––Àƒ±þ–Œ£¨“‘OŒ™‘≤–ƒ£¨OAŒ™∞Îæ∂µƒ‘≤ΩªAB”⁄D£¨—”≥§AOΩª°—O”⁄E£¨¡¨Ω”CD£¨CE£¨»ÙCE «°—Oµƒ«–œþ£¨Ω‚¥œ¬¡–Œ £∫
£®1£©«Û÷§£∫CD «°—Oµƒ«–œþ£ª
£®2£©»ÙBC=3£¨CD=4£¨«Û∆Ω––Àƒ±þ–ŒOABCµƒ√ʪ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ„ƒÐ«Û![]() µƒ÷µ¬?”ˆµΩ’‚—˘µƒŒ £¨Œ“√«ø…“‘œ»Àºøº“ªœ¬£¨¥”ºÚµ•µƒ«È–Œ»Î ÷£Æœ»∑÷±º∆À„œ¬¡–∏˜ Ωµƒ÷µ£Æ
µƒ÷µ¬?”ˆµΩ’‚—˘µƒŒ £¨Œ“√«ø…“‘œ»Àºøº“ªœ¬£¨¥”ºÚµ•µƒ«È–Œ»Î ÷£Æœ»∑÷±º∆À„œ¬¡–∏˜ Ωµƒ÷µ£Æ
¢Ÿ![]()
¢⁄![]()
¢€![]() °≠°≠
°≠°≠
£®1£©”…¥ÀŒ“√«ø…“‘µ√µΩ£∫![]()
«Îƒ„¿˚”√…œ√ʵƒΩ·¬€£¨‘ŸÕÍ≥…œ¬√Ê¡Ωµƒº∆À„£∫
£®2£©250+249+248+°≠+22+2+1
£®3£©»Ù![]() £¨«Ûx2020µƒ÷µ
£¨«Ûx2020µƒ÷µ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øΩ‚œ¬¡–∑Ω≥Ã◊È”Î≤ªµ» Ω£®◊È£©
£®1£©Ω‚∑Ω≥Ã◊È![]() £ª
£ª
£®2£©Ω‚≤ªµ» Ω◊È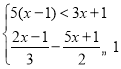 £ª
£ª
£®3£©Ω‚≤ªµ» Ωx-![]()
![]() ≤¢∞—Ω‚ºØ‘⁄ ˝÷·…œ±Ì æ≥ˆ¿¥£Æ
≤¢∞—Ω‚ºØ‘⁄ ˝÷·…œ±Ì æ≥ˆ¿¥£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄œ¬¡–∏˜◊ÈÃıº˛÷–£¨≤ªƒÐÀµ√˜![]() µƒ «£® £©
µƒ «£® £©
A.AB=DE£¨°œB=°œE£¨°œC=°œFB.AB=DE£¨°œA=°œD£¨°œB=°œE
C.AC=DF£¨BC=EF£¨°œA=°œDD.AB=DE£¨BC=EF£¨AC=ED
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄°˜ABC÷–£¨±þAB°¢ACµƒ¥π÷±∆Ω∑÷œþ∑÷±ΩªBC”⁄D°¢E£Æ
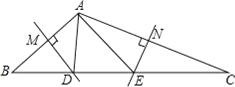
£®1£©»ÙBC=10£¨«Û°˜ADEµƒ÷Ð≥§£ª
£®2£© …Ë÷±œþDM°¢ENΩª”⁄µ„O
¢Ÿ ‘≈–∂œµ„O «∑Ò‘⁄BCµƒ¥π÷±∆Ω∑÷œþ…œ£¨≤¢Àµ√˜¿Ì”…£ª
¢⁄»Ù°œBAC=100°„£¨«Û°œBOCµƒ∂» ˝
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“ª¥Œ∫Ø ˝y£Ω©Å2x+4µƒÕºœÛ”Îx÷·°¢y÷·∑÷±Ωª”⁄µ„A°¢B£¨µ„C «OAµƒ÷–µ„£¨π˝µ„C◊˜CD°ÕOA”⁄CΩª“ª¥Œ∫Ø ˝ÕºœÛ”⁄µ„D£¨P «OB…œ“ª∂ص„£¨‘ÚPC+PDµƒ◊Ó–°÷µŒ™£®°°°°£©

A.4B.![]() C.2
C.2![]() D.2
D.2![]() +2
+2
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com