
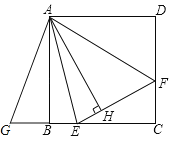
【题目】如图,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H,将△ADF绕点A顺时针旋转90°得到△ABG,若BE=2,DF=3,则AH的长为______.
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
【题目】
已知:等边三角形ABC
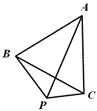
(1)如图1,P为等边△ABC外一点,且∠BPC=120°.试猜想线段BP、PC、AP之间的数量关系,并证明你的猜想;
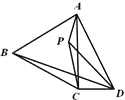
(2)如图2,P为等边△ABC内一点,且∠APD=120°.求证:PA+PD+PC>BD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
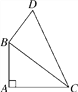
【题目】如图所示,在四边形ABDC中,∠A=90°,AB=9,AC=12,BD=8,CD=17.
(1)连接BC,求BC的长;
(2)求四边形ABDC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为改善城市排水系统,某市需要新铺设一段全长为![]() 的排水管道.为了减少施工对城市交通的影响,实际施工时每天的工效是原计划的
的排水管道.为了减少施工对城市交通的影响,实际施工时每天的工效是原计划的![]() 倍,结果提前
倍,结果提前![]() 天完成这一任务.
天完成这一任务.
(1)这个工程队原计划每天铺设管道多少![]() ?
?
(2)在这项工程中,如果要求工程队提前![]() 天完成任务,那么实际施工时每天的工效比原计划增加的百分率是多少?
天完成任务,那么实际施工时每天的工效比原计划增加的百分率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
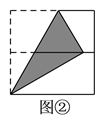
【题目】如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形(阴影部分),且它的一条直角边等于斜边的一半,这样的图形有( ).



A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,![]() 为
为![]() 轴负半轴上的点,
轴负半轴上的点,![]() 为
为![]() 轴负半轴上的点.
轴负半轴上的点.
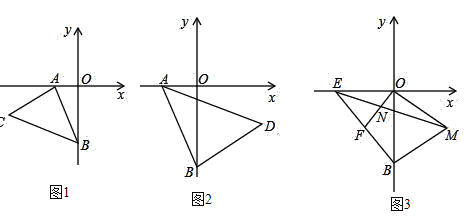
(1)如图1,以![]() 点为顶点、
点为顶点、![]() 为腰在第三象限作等腰
为腰在第三象限作等腰![]() ,若
,若![]() ,
,![]() ,试求
,试求![]() 点的坐标;
点的坐标;
(2)如图![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的纵坐标为
的纵坐标为![]() ,以
,以![]() 为顶点,
为顶点,![]() 为腰作等腰
为腰作等腰![]() .试问:当
.试问:当![]() 点沿
点沿![]() 轴负半轴向下运动且其他条件都不变时,整式
轴负半轴向下运动且其他条件都不变时,整式![]() 的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由;
的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由;
(3)如图![]() ,
,![]() 为
为![]() 轴负半轴上的一点,且
轴负半轴上的一点,且![]() ,
,![]() 于点
于点![]() ,以
,以![]() 为边作等边
为边作等边![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,试探索:在线段
,试探索:在线段![]() 、
、![]() 和
和![]() 中,哪条线段等于
中,哪条线段等于![]() 与
与![]() 的差的一半?请你写出这个等量关系,并加以证明.
的差的一半?请你写出这个等量关系,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com