
 如图,抛物线y=-x2+3x+4与x轴交于点A,B,与y轴交于点C,P(m,n)为第一象限内抛物线上的一点,点D的坐标为(0,6).
如图,抛物线y=-x2+3x+4与x轴交于点A,B,与y轴交于点C,P(m,n)为第一象限内抛物线上的一点,点D的坐标为(0,6).分析 (1)根据y=0时,即-x2+3x+4=0,求出x的值,即可确定点A,点B坐标,即可求出OB;由抛物线的顶点式,即可确定抛物线的顶点坐标;
(2)连接CP,CP′,先求出m的值,确定这时P点的坐标为(3,4),再确定点D的坐标,求出∠OCB=45°=∠BCP,从而确定点P′在y轴上,且CP′=CP=3,即可解答.
(3)存在,根据直线PD所对应的一次函数随x的增大而增大,所以一次函数的图象一定经过一、三象限,即可得到1<m<2.
解答 解:(1)当y=0时,即-x2+3x+4=0,
解得:x1=4,x2=-1,
∴点A(-1,0)点B(4,0),
∴OB=4,
y=-x2+3x+4=$-(x-\frac{3}{2})^{2}+\frac{25}{4}$,
∴抛物线的顶点坐标为($\frac{3}{2}$,$\frac{25}{4}$),
故答案为:4,($\frac{3}{2}$,$\frac{25}{4}$).
(2)如图,连接CP,CP′,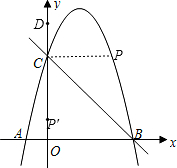
n=4时,-m2+3m+4=4,
解得:m1=3,m2=0(舍去),
∴这时P点的坐标为(3,4),
∵OC=4,
∴CP∥x轴,CP=3,
∵点C的坐标为(0,4),
∴OB=OC=4,
∴∠OCB=45°=∠BCP,
∴点P′在y轴上,且CP′=CP=3,
∴P′的坐标为(0,1).
(3)存在,
∵点D的坐标为(0,6),
∴当y=6时,-x2+3x+4=6,
解得:x1=1,x2=2,
∵直线PD所对应的一次函数随x的增大而增大,
∴一次函数的图象一定经过一、三象限,
∴1<m<2.
点评 本题考查了二次函数的性质、等腰直角三角形的性质、一次函数的性质、点的对称,解决本题的关键是熟记二次函数的性质、一次函数的性质.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:填空题
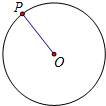 如图所示,⊙O的面积为1,点P为⊙O上一点,令记号[n,m]表示半径OP从如图所示的位置开始以点O为中心连续旋转n次后,半径OP扫过的面积.旋转的规则为:第1次旋转m度;第2次从第1次停止的位置向相同的方向再次旋转$\frac{m}{2}$度;第3次从第2次停止的位置向相同的方向再次旋转$\frac{m}{4}$度;第4次从第3次停止的位置向相同的方向再次旋转$\frac{m}{8}$度;…依此类推.例如[2,90]=$\frac{3}{8}$,则[2016,180]=$\frac{{2}^{2016}-1}{{2}^{2016}}$.
如图所示,⊙O的面积为1,点P为⊙O上一点,令记号[n,m]表示半径OP从如图所示的位置开始以点O为中心连续旋转n次后,半径OP扫过的面积.旋转的规则为:第1次旋转m度;第2次从第1次停止的位置向相同的方向再次旋转$\frac{m}{2}$度;第3次从第2次停止的位置向相同的方向再次旋转$\frac{m}{4}$度;第4次从第3次停止的位置向相同的方向再次旋转$\frac{m}{8}$度;…依此类推.例如[2,90]=$\frac{3}{8}$,则[2016,180]=$\frac{{2}^{2016}-1}{{2}^{2016}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
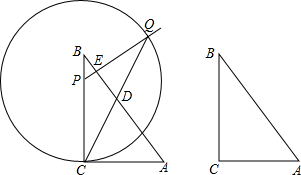
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
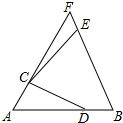 如图,等边△ABF中,点C,D分别在AF、AB上,线段CD绕点C逆时针旋转60°到线段CE,点E恰好落在BF上.
如图,等边△ABF中,点C,D分别在AF、AB上,线段CD绕点C逆时针旋转60°到线段CE,点E恰好落在BF上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com