
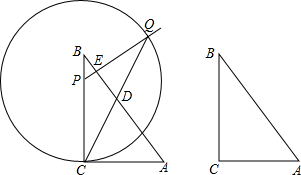
分析 (1)易证AD=AC,只需运用三角函数和勾股定理求出AC即可;
(2)过点Q作QH⊥BC于H,如图1,只需用x的代数式表示QH就可解决问题;
(3)由于△PQF是以PF为腰的等腰三角形,故需分PF=PQ和PF=FQ两种情况讨论,只需将等腰三角形的性质和三角函数相结合,就可解决问题.
解答 解:(1)在Rt△ABC中,
∵∠ACB=90°,AB=5,sinA=$\frac{4}{5}$,
∴BC=AB•sinA=5×$\frac{4}{5}$=4,
∴AC=$\sqrt{{5}^{2}-{4}^{2}}$=3.
∵PC=PQ,∴∠PCQ=∠PQC.
∵PE⊥AB即∠QED=90°,
∴∠EQD+∠EDQ=90°.
∵∠ACD+∠PCQ=90°,
∴∠EDQ=∠ACD.
∵∠CDA=∠EDQ,
∴∠ACD=∠CDA,
∴AD=AC=3;
(2)过点Q作QH⊥BC于H,如图1,
∵∠PBE+∠BPE=90°,∠PBE+∠A=90°,
∴∠BPE=∠A,
∴sin∠HPQ=sin∠A=$\frac{4}{5}$,
∴sin∠HPQ=$\frac{QH}{PQ}$=$\frac{4}{5}$.
∵PQ=PC=x,∴QH=$\frac{4}{5}$x,
∴S△PCQ=$\frac{1}{2}$PC•QH=$\frac{1}{2}$x•$\frac{4}{5}$x=$\frac{2}{5}$x2($\frac{3}{2}$≤x<4);
(当E、Q、D共线时,可得x最小值,根据$\frac{x}{4-x}$=$\frac{3}{5}$,解得x=$\frac{3}{2}$.)
(3)①当PF=PQ时,则有PF=PQ=x=PC.
过点P作PG⊥CF于G,如图2,
则CG=$\frac{1}{2}$CF.
∵CF⊥AB,
∴S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CF,
∴CF=$\frac{3×4}{5}$=$\frac{12}{5}$,
∴CG=$\frac{6}{5}$.
∵∠PCG=90°-∠FCA=∠A,
∴cos∠PCG=cos∠A=$\frac{3}{5}$,
∴cos∠PCG=$\frac{CG}{PC}$=$\frac{3}{5}$,
∴x=PC=$\frac{5}{3}$CG=$\frac{5}{3}$×$\frac{6}{5}$=2;
②当PF=FQ时,
∵FE⊥PQ,
∴PE=$\frac{1}{2}$PQ=$\frac{1}{2}$x,
∴cos∠BPE=$\frac{PE}{BP}$=$\frac{\frac{1}{2}x}{4-x}$=$\frac{3}{5}$,
∴x=$\frac{24}{11}$.
综上所述:当△PQF是以PF为腰的等腰三角形,CP的长为2或$\frac{24}{11}$.
点评 本题主要考查了等腰三角形的判定与性质、三角函数、同角或等角的余角相等、勾股定理等知识,运用分类讨论的思想是解决第(3)小题的关键.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:解答题
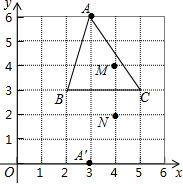 如图所示,△ABC和△A′BC存在着某种对应关系(它们关于BC对称),其中A的对应点是A′,A(3,6),A′(3,0),△ABC内部的点M(4,4)的对应点是N(4,2).
如图所示,△ABC和△A′BC存在着某种对应关系(它们关于BC对称),其中A的对应点是A′,A(3,6),A′(3,0),△ABC内部的点M(4,4)的对应点是N(4,2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
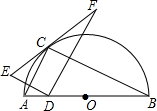 如图,点C在以AB为直径的半圆上,AB=4,∠CBA=30°,点D在AO上运动,点E与点D关于AC对称:DF⊥DE于点D,并交EC的延长线于点F,下列结论:
如图,点C在以AB为直径的半圆上,AB=4,∠CBA=30°,点D在AO上运动,点E与点D关于AC对称:DF⊥DE于点D,并交EC的延长线于点F,下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB=AC,∠A=40°,将△ABC绕点B逆时针旋转得到△A′BC′,若点C的对应点C′落在AB边上,则旋转角为( )
如图,在△ABC中,AB=AC,∠A=40°,将△ABC绕点B逆时针旋转得到△A′BC′,若点C的对应点C′落在AB边上,则旋转角为( )| A. | 40° | B. | 70° | C. | 80° | D. | 140° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
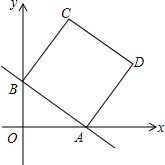 如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+b分别与x轴、y轴交于点A、B,且点A的坐标为(4,0),四边形ABCD是正方形.
如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+b分别与x轴、y轴交于点A、B,且点A的坐标为(4,0),四边形ABCD是正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-x2+3x+4与x轴交于点A,B,与y轴交于点C,P(m,n)为第一象限内抛物线上的一点,点D的坐标为(0,6).
如图,抛物线y=-x2+3x+4与x轴交于点A,B,与y轴交于点C,P(m,n)为第一象限内抛物线上的一点,点D的坐标为(0,6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠ABC=50°,∠ACB=60°,∠ABC与∠ACB的平分线交于点O,过O作DE∥BC,交AB、AC于点D、E,求∠BOC的度数.
如图,∠ABC=50°,∠ACB=60°,∠ABC与∠ACB的平分线交于点O,过O作DE∥BC,交AB、AC于点D、E,求∠BOC的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com