
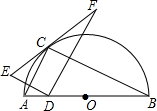
 如图,点C在以AB为直径的半圆上,AB=4,∠CBA=30°,点D在AO上运动,点E与点D关于AC对称:DF⊥DE于点D,并交EC的延长线于点F,下列结论:
如图,点C在以AB为直径的半圆上,AB=4,∠CBA=30°,点D在AO上运动,点E与点D关于AC对称:DF⊥DE于点D,并交EC的延长线于点F,下列结论:分析 (1)由点E与点D关于AC对称可得CE=CD,再根据DF⊥DE即可证到CE=CF.
(2)根据“点到直线之间,垂线段最短”可得CD⊥AB时CD最小,由于EF=2CD,求出CD的最小值就可求出EF的最小值.
(3)连接OC,易证△AOC是等边三角形,AD=OD,根据等腰三角形的“三线合一”可求出∠ACD,进而可求出∠ECO=90°,从而得到EF与半圆相切.
(4)首先根据对称性确定线段EF扫过的图形,然后探究出该图形与△ABC的关系,就可求出线段EF扫过的面积.
解答 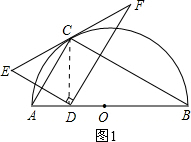 解:①连接CD,如图1所示.
解:①连接CD,如图1所示.
∵点E与点D关于AC对称,
∴CE=CD.
∴∠E=∠CDE.
∵DF⊥DE,
∴∠EDF=90°.
∴∠E+∠F=90°,∠CDE+∠CDF=90°.
∴∠F=∠CDF.
∴CD=CF,
∴CE=CD=CF.故①正确.
②当CD⊥AB时,如图2所示.
∵AB是半圆的直径,
∴∠ACB=90°.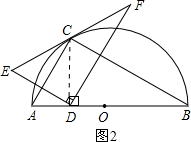
∵AB=4,∠CBA=30°,
∴∠CAB=60°,AC=2,BC=2$\sqrt{3}$.
∵CD⊥AB,∠CBA=30°,
∴CD=$\frac{1}{2}$BC=$\sqrt{3}$.
根据“点到直线之间,垂线段最短”可得:
点D在线段AB上运动时,CD的最小值为$\sqrt{3}$.
∵CE=CD=CF,
∴EF=2CD.
∴线段EF的最小值为2$\sqrt{3}$.故②错误.
③当AD=1时,连接OC,如图3所示.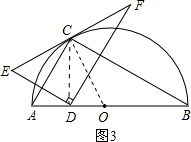
∵OA=OC,∠CAB=60°,
∴△OAC是等边三角形.
∴CA=CO,∠ACO=60°.
∵AO=2,AD=1,
∴DO=1.
∴AD=DO,
∴∠ACD=∠OCD=30°,
∵点E与点D关于AC对称,
∴∠ECA=∠DCA,
∴∠ECA=30°,
∴∠ECO=90°,
∴OC⊥EF,
∵EF经过半径OC的外端,且OC⊥EF,
∴EF与半圆相切.故③正确.
④∵点D与点E关于AC对称,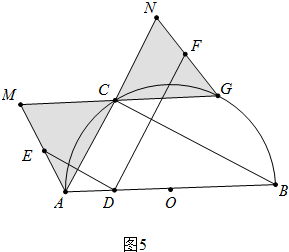
点D与点F关于BC对称,
∴当点D从点A运动到点O时,
点E的运动路径AM与AO关于AC对称,
点F的运动路径NG与AO关于BC对称.
∴EF扫过的图形就是图5中阴影部分.
∴S阴影=2S△AOC=2×$\frac{1}{4}$•AC•BC=$2\sqrt{3}$=2$\sqrt{3}$.故④错误.
故答案为①③.
点评 本题考查了等边三角形的判定与性质、平行线的判定与性质、相似三角形的判定与性质、切线的判定、轴对称的性质、含30°角的直角三角形、垂线段最短等知识,综合性强,有一定的难度,第四个问题解题的关键是通过特殊点探究EF的运动轨迹,属于中考压轴题.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
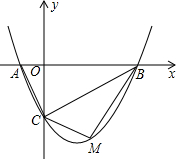 如图,二次函数y=ax2-$\frac{3}{2}$x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知点A(-1,0),点C(0,-2).
如图,二次函数y=ax2-$\frac{3}{2}$x+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,已知点A(-1,0),点C(0,-2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
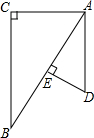 如图,在△ABC和△ADE中,∠C=∠AED=90°,点E在线段AB上,AD∥CB,若AC=AE=2,BC=3,则DE的长为$\frac{4}{3}$.
如图,在△ABC和△ADE中,∠C=∠AED=90°,点E在线段AB上,AD∥CB,若AC=AE=2,BC=3,则DE的长为$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
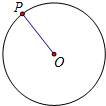 如图所示,⊙O的面积为1,点P为⊙O上一点,令记号[n,m]表示半径OP从如图所示的位置开始以点O为中心连续旋转n次后,半径OP扫过的面积.旋转的规则为:第1次旋转m度;第2次从第1次停止的位置向相同的方向再次旋转$\frac{m}{2}$度;第3次从第2次停止的位置向相同的方向再次旋转$\frac{m}{4}$度;第4次从第3次停止的位置向相同的方向再次旋转$\frac{m}{8}$度;…依此类推.例如[2,90]=$\frac{3}{8}$,则[2016,180]=$\frac{{2}^{2016}-1}{{2}^{2016}}$.
如图所示,⊙O的面积为1,点P为⊙O上一点,令记号[n,m]表示半径OP从如图所示的位置开始以点O为中心连续旋转n次后,半径OP扫过的面积.旋转的规则为:第1次旋转m度;第2次从第1次停止的位置向相同的方向再次旋转$\frac{m}{2}$度;第3次从第2次停止的位置向相同的方向再次旋转$\frac{m}{4}$度;第4次从第3次停止的位置向相同的方向再次旋转$\frac{m}{8}$度;…依此类推.例如[2,90]=$\frac{3}{8}$,则[2016,180]=$\frac{{2}^{2016}-1}{{2}^{2016}}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
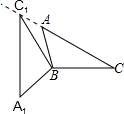 如图,在△ABC中,∠ACB=30°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1,当点C1在线段CA的延长线上时,则∠CC1A1=60°.
如图,在△ABC中,∠ACB=30°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1,当点C1在线段CA的延长线上时,则∠CC1A1=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
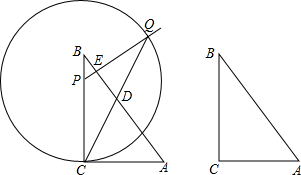
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,矩形ABCD的对角线相交于点O,
已知:如图,矩形ABCD的对角线相交于点O,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com