

���� ��1�������ߵ����ʣ��á�OPQ�ǵȱ������Σ�Ȼ��ȱ������ε������Լ����Ǻ�����֪ʶ������⣬������ô𰸣�
��2��n��Բ��ֱ����Ϊ���еĸߣ���ϣ�1�����ɵȱ������ε����ʺ��ɶ������м�����еĸߣ�
��3����ϣ�2���Ľ��۽��з���������ô𰸣�
���  �⣺��1������OA��
�⣺��1������OA��
������ֱ��Ϊa�ĵ�Բ��P����Q����O�������У�
��OP=PQ=OQ=a��
���OPQ�ǵȱ������Σ�
���OPQ=60�㣬
��AP=AQ��
��OA��PQ��
��OA=OP•sin60��=$\frac{\sqrt{3}}{2}$a��
�ʴ�Ϊ��$\frac{{\sqrt{3}}}{2}a$��
��2����ͼ�ڣ��߶�hn=na��
��ͼ�ۣ�h��n=$\frac{\sqrt{3}}{2}$��n-1��a+a��
�ʴ�Ϊ��na��$\frac{\sqrt{3}}{2}$��n-1��a+a��
��3�������������ּ�װ����װ��ͭ�����࣮
���ɣ�����һ��0.1n��2.5��
��ã�n��25��
25��25=625��
���������������⣬��һ���ŷ�25�����ڶ����ŷ�24����
��ֹܵķ��ò���Ϊn���ɵ�$\frac{\sqrt{3}}{2}$��n-1����0.1+0.1��2.5��
���n��28.7��
��n��������
��n=28��
�ֹܷ��õ�������Ϊ��25��14+24��14=686��������
����������ּ�װ����װ��ͭ�����࣮
���� ��������Բ���ۺ��⣮���������ߵ����ʡ��ȱ������ε��ж��������Լ����Ǻ�����֪ʶ��ע��õ�����h��n=$\frac{\sqrt{3}}{2}$��n-1��a+a�ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
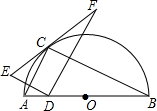 ��ͼ����C����ABΪֱ���İ�Բ�ϣ�AB=4����CBA=30�㣬��D��AO���˶�����E���D����AC�Գƣ�DF��DE�ڵ�D������EC���ӳ����ڵ�F�����н��ۣ�
��ͼ����C����ABΪֱ���İ�Բ�ϣ�AB=4����CBA=30�㣬��D��AO���˶�����E���D����AC�Գƣ�DF��DE�ڵ�D������EC���ӳ����ڵ�F�����н��ۣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
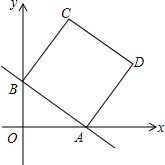 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-$\frac{3}{4}$x+b�ֱ���x�ᡢy�ύ�ڵ�A��B���ҵ�A������Ϊ��4��0�����ı���ABCD�������Σ�
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=-$\frac{3}{4}$x+b�ֱ���x�ᡢy�ύ�ڵ�A��B���ҵ�A������Ϊ��4��0�����ı���ABCD�������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������y=-x2+3x+4��x�ύ�ڵ�A��B����y�ύ�ڵ�C��P��m��n��Ϊ��һ�������������ϵ�һ�㣬��D������Ϊ��0��6����
��ͼ��������y=-x2+3x+4��x�ύ�ڵ�A��B����y�ύ�ڵ�C��P��m��n��Ϊ��һ�������������ϵ�һ�㣬��D������Ϊ��0��6�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC=50�㣬��ACB=60�㣬��ABC���ACB��ƽ���߽��ڵ�O����O��DE��BC����AB��AC�ڵ�D��E�����BOC�Ķ�����
��ͼ����ABC=50�㣬��ACB=60�㣬��ABC���ACB��ƽ���߽��ڵ�O����O��DE��BC����AB��AC�ڵ�D��E�����BOC�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com