
【题目】计算
(1)(4﹣π)0+|﹣2|﹣16×4﹣1+ ![]() ÷
÷ ![]()
(2)![]() ÷
÷ ![]() ﹣2
﹣2 ![]() ×
× ![]() +
+ ![]() .
.
【答案】
(1)解:原式=1+2﹣16× ![]() +
+ ![]()
=1+2﹣4+2
=1;
(2)解:原式= ![]() ﹣2
﹣2 ![]() +2
+2 ![]()
=4﹣2 ![]() +2
+2 ![]()
=4.
【解析】(1)先根据零指数幂和负整数指数幂的意义计算,然后进行二次根式的除法运算,然后合并即可;(2)先根据二次根式的乘除法法则运算,然后化简后合并即可.
【考点精析】根据题目的已知条件,利用零指数幂法则和整数指数幂的运算性质的相关知识可以得到问题的答案,需要掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数).


科目:初中数学 来源: 题型:
【题目】“五一”期间,甲、乙两家商店以同样价格销售相同的商品,两家优惠方案分别为:甲店一次性购物中超过200元后的价格部分打七折;乙店一次性购物中超过500元后的价格部分打五折,设商品原价为x元(x≥0),购物应付金额为y元. 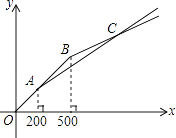
(1)求在甲商店购物时y与x之间的函数关系;
(2)两种购物方式对应的函数图象如图所示,求交点C的坐标;
(3)根据图象,请直接写出“五一”期间选择哪家商店购物更优惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD. 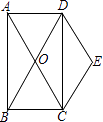
(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形ABCD中,AB=2,BC=1,动点P从点B出发,沿路线B→C→D做匀速运动,那么△ABP的面积S与点P运动的路程x之间的函数图象大致为( )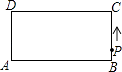
A.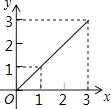
B.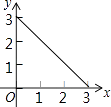
C.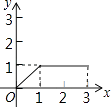
D.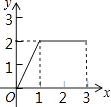
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学课上,同学们已经探究过“经过已知直线外一点作这条直线的垂线”的尺规作图过程:
已知:直线
求作:直线 做法:如图:(1)在直线 (2)分别以点 (3)作直线 |
参考以上材料作图的方法,解决以下问题:
(1)以上材料作图的依据是 .
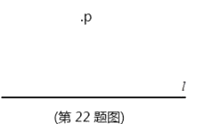
(3)已知:直线![]() 和
和![]() 外一点
外一点![]() ,
,
求作:![]() ,使它与直线
,使它与直线![]() 相切。(尺规作图,不写做法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
相切。(尺规作图,不写做法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩(成绩![]() 取整数,总分100分)作为样本进行统计,制成如下不完整的统计图表:
取整数,总分100分)作为样本进行统计,制成如下不完整的统计图表:
频数频率分布表
成绩 | 频数(人) | 频率 |
| 10 | 0.05 |
| 30 | 0.15 |
| 40 |
|
|
| 0.35 |
| 50 | 0.25 |
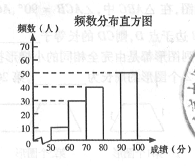
根据所给信息,解答下列问题:
(1)![]() _____________,
_____________,![]() ______________;
______________;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在______________分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,点
,点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
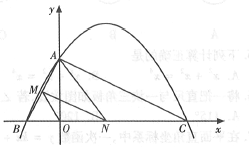
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接![]() ,若点
,若点![]() 在线段
在线段![]() 上运动(不与点
上运动(不与点![]() 重合),过点
重合),过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,当
,当![]() 面积最大时,求N点的坐标;
面积最大时,求N点的坐标;
(3)连接![]() ,在(2)的结论下,求
,在(2)的结论下,求![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与证明: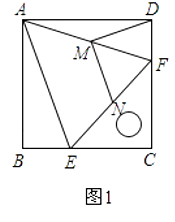
如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.
(1)连接AE,求证:△AEF是等腰三角形;
猜想与发现:
(2)在(1)的条件下,请判断线段MD与MN的关系,得出结论;
结论:DM、MN的关系是:;
拓展与探究:
(3)如图2,将图1中的直角三角板ECF绕点C旋转180°,其他条件不变,则(2)中的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.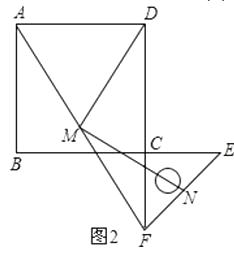
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com