
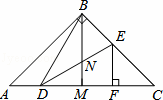
如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边中线,点D,E分别在边AC和BC上,DB=DE,EF⊥AC于点F,以下结论:
(1)∠DBM=∠CDE; (2)S△BDE<S四边形BMFE;
(3)CD•EN=BN•BD; (4)AC=2DF.
其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
C. 解:(1)设∠EDC=x,则∠DEF=90°﹣x
∴∠DBE=∠DEB=∠EDC+∠C=x+45°,
∵BD=DE,
∴∠DBM=∠DBE﹣∠MBE=45°+x﹣45°=x.
∴∠DBM=∠CDE,故(1)正确;
(2)在Rt△BDM和Rt△DEF中,
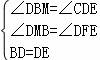 ,
,
∴Rt△BDM≌Rt△DEF.
∴S△BDM=S△DEF.
∴S△BDM﹣S△DMN=S△DEF﹣S△DMN,即S△DBN=S四边形MNEF.
∴S△DBN+S△BNE=S四边形MNEF+S△B NE,
NE,
∴S△BDE=S四边形BMFE,故(2)错误;
(3)∵∠BNE=∠DBM+∠BDN,∠BDM=∠BDE+∠EDF,∠EDF=∠DBM,
∴∠BNE=∠BDM.
又∵∠C=∠NBE=45°
∴△DBC∽△NEB.
∴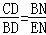 ,
,
∴CD•EN=BN•BD;故(3)正确;
(4)∵Rt△BDM≌Rt△DEF,
∴BM=DF,
∵∠B=90°,M是AC的中点,
∴BM=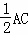 .
.
∴DF=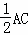 ,故(4)正确.
,故(4)正确.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
一组数1,1,2,x,5,y,…,满足“从第三个数起,每个数都等于它前面的两个数之和”,那么这组数中y表示的数为
A.8 B.9 C.13 D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
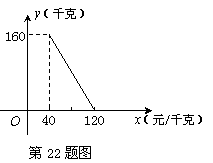
某商店以40元/千克的单价新进一批茶叶,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示.
(1)根据图象求y与x的函数关系式;
(2)商店想在销 售成本不超过3000元的情况下,使销售利润达到2400元,销售单价应定为多少?
售成本不超过3000元的情况下,使销售利润达到2400元,销售单价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线y=x2+bx+c经过点A(﹣1,0),B(3,0).请解答下列问题:
(1)求抛物线的解析式;
(2)点E(2,m)在抛物线上,抛物线的对称轴与x轴交于点H,点F是AE中点,连接FH,求线段FH的长.
注:抛物线y=ax2+bx+c(a≠0)的对称轴是x=﹣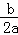 .
.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级下学期第一次学情调研数学试卷(解析版) 题型:填空题
已知点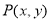 位于第二象限,并且
位于第二象限,并且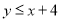 ,
,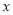 、
、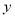 为整数,若以
为整数,若以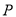 为圆心,
为圆心,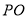 为半径画圆,则可以画出 个半径不同的圆来。
为半径画圆,则可以画出 个半径不同的圆来。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市江都区七校联谊九年级3月月考数学试卷(解析版) 题型:选择题
函数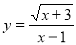 中自变量x的取值范围是( )
中自变量x的取值范围是( )
A.x≥-3 B.x≥-3且x≠1 C.x≠1 D.x≠-3且x≠1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com