
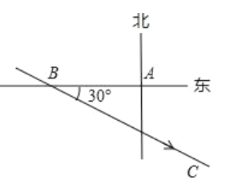
【题目】温州市处于东南沿海,夏季经常遭受台风袭击,一次,温州气象局测得台风中心在温州市![]() 的正西方向300千米的
的正西方向300千米的![]() 处,以每小时
处,以每小时![]() 千米的速度向东偏南
千米的速度向东偏南![]() 的
的![]() 方向移动,距台风中心200千米的范围是受台风严重影响的区域,试问:
方向移动,距台风中心200千米的范围是受台风严重影响的区域,试问:
(1)台风中心在移动过程中离温州市最近距离是多少千米?
(2)温州市![]() 是否受台风影响?若不会受到,请说明理由;若会受到,求出温州市受台风严重影响的时间.
是否受台风影响?若不会受到,请说明理由;若会受到,求出温州市受台风严重影响的时间.
【答案】(1)过点A作AD⊥BC于D,
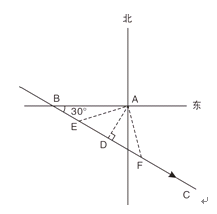
由题意得 AB=300,∠ABD=300
∴AD=![]() AB=150(km)…………(4分)
AB=150(km)…………(4分)
(2)∵150<200
∴温州市点A受到台风严重影响
设风台中心距A点200km处,刚好处在BC上的E,F两点 则
在Rt△ADE中,AE=200,AD=150
∴DE=![]() =
=![]()
∴EF=2DE=![]()
∴温州市A受台风严重影响的时间为![]() …………(10分)
…………(10分)
【解析】
本题可利用直角三角形性质来解,(1)先作出点A到BC的垂线,就求出了台风中心距A市的最短距离;
(2)求出最短距离和200米相比,可以看到最短距离小于200米,可见A市会受到台风影响,然后再向BC作两条交BC时长为200千米的辅助线,解直角三角形即可.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】下列一定是一元二次方程的有( )
(1)(a-1)x+bx+c=0(a,b,c是实数);(2)2x+![]() +3=0;(3)(1-2x)(3-x)=2x+1;(4)x+2x-y=0;(5)
+3=0;(3)(1-2x)(3-x)=2x+1;(4)x+2x-y=0;(5)![]() x-8=
x-8=![]() x
x
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中国梦”关乎每个人的幸福生活,为进一步感知我们身边的幸福,展现成都人追梦的风采,我市某校开展了以“梦想中国,逐梦成都”为主题的摄影大赛,要求参赛学生每人交一件作品.现将参赛的50件作品的成绩(单位:分)进行统计如下:
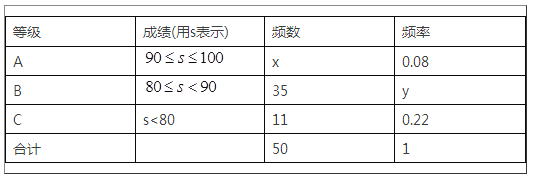
请根据上表提供的信息,解答下列问题:
(1)表中x的值为________,y的值为________;
(2)将本次参赛作品获得A等级的学生依次用A1,A2,A3,…表示,现该校决定从本次参赛作品获得A等级的学生中,随机抽取两名学生谈谈他们的参赛体会,请用树状图或列表法求恰好抽到学生A1和A2的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年6月份,某果农收获荔枝30吨,香蕉13吨,现计划租用甲、乙两种货车共10辆将这批水果全部运往港口,已知一辆甲种货车可装荔枝和香蕉共5吨,且一辆甲种货车可装的荔枝重量(单位:吨)是其可装的香蕉重量的4倍,一辆乙种货车可装荔枝香蕉各2吨;
(1)一辆甲种货车可装载荔枝、香蕉各多少吨?
(2)该果农安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)若甲种货车每辆要付运输费2000元,乙种货车每辆要付运输费1300元,则该果农应选择哪种方案?使运费最少?最少运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:在数学活动课上,老师出示了这样一个问题:如图1,在矩形ABCD中,AD=2AB,E是AB延长线上一点,且BE=AB,连接DE,交BC于点M,以DE为一边在DE的左下方作正方形DEFG,连接AM.试判断线段AM与DE的位置关系.
探究展示:勤奋小组发现,AM垂直平分DE,并展示了如下的证明方法:
证明:∵BE=AB,∴AE=2AB.
∵AD=2AB,∴AD=AE.
∵四边形ABCD是矩形,∴AD∥BC.
∴![]() .(依据1)
.(依据1)
∵BE=AB,∴![]() .∴EM=DM.
.∴EM=DM.
即AM是△ADE的DE边上的中线,
又∵AD=AE,∴AM⊥DE.(依据2)
∴AM垂直平分DE.
反思交流:
(1)①上述证明过程中的“依据1”“依据2”分别是指什么?
②试判断图1中的点A是否在线段GF的垂直平分线上,请直接回答,不必证明;
(2)创新小组受到勤奋小组的启发,继续进行探究,如图2,连接CE,以CE为一边在CE的左下方作正方形CEFG,发现点G在线段BC的垂直平分线上,请你给出证明;
探索发现:
(3)如图3,连接CE,以CE为一边在CE的右上方作正方形CEFG,可以发现点C,点B都在线段AE的垂直平分线上,除此之外,请观察矩形ABCD和正方形CEFG的顶点与边,你还能发现哪个顶点在哪条边的垂直平分线上,请写出一个你发现的结论,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,AB=4,点
,AB=4,点![]() 是边
是边![]() 上动点(点
上动点(点![]() 不与点
不与点![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() ,交
,交![]() 边于点
边于点![]() .
.
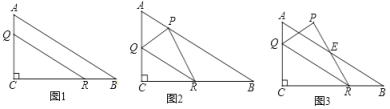
(1)求![]() 的大小;
的大小;
(2)若把![]() 沿着直线
沿着直线![]() 翻折得到
翻折得到![]() ,设
,设![]()
① 如图2,当点![]() 落在斜边
落在斜边![]() 上时,求
上时,求![]() 的值;
的值;
② 如图3,当点![]() 落在
落在![]() 外部时,
外部时,![]() 与
与![]() 相交于点
相交于点![]() ,如果
,如果![]() ,写出
,写出![]() 与
与![]() 的函数关系式以及定义域.
的函数关系式以及定义域.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若△ABC内一点P满足∠PAC=∠PCB=∠PBA,则称点P为△ABC的布罗卡尔点,三角形的布罗卡尔点是法国数学家和数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,布罗卡尔点的再次发现,引发了研究“三角形几何”的热潮.已知△ABC中,CA=CB,∠ACB=120°,P为△ABC的布罗卡尔点,若PA=![]() ,则PB+PC=_____.
,则PB+PC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣.已知购买甲型机器人1台,乙型机器人2台,共需14万元;购买甲型机器人2台,乙型机器人3台,共需24万元.
(1)求甲、乙两种型号的机器人每台的价格各是多少万元;
(2)已知甲型和乙型机器人每台每小时分拣快递分别是1200件和1000件,该公司计划购买这两种型号的机器人共8台,总费用不超过41万元,并且使这8台机器人每小时分拣快递件数总和不少于8300件,则该公司有哪几种购买方案?哪个方案费用最低,最低费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
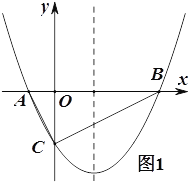
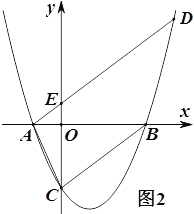
【题目】如图,已知抛物线![]() (
(![]() >0)与
>0)与![]() 轴交于A,B两点(A点在B点的左边),与
轴交于A,B两点(A点在B点的左边),与![]() 轴交于点C。
轴交于点C。
(1)如图1,若△ABC为直角三角形,求![]() 的值;
的值;
(2)如图1,在(1)的条件下,点P在抛物线上,点Q在抛物线的对称轴上,若以BC为边,以点B,C,P,Q为顶点的四边形是平行四边形,求P点的坐标;
(3)如图2,过点A作直线BC的平行线交抛物线于另一点D,交![]() 轴交于点E,若AE:ED=1:4,求
轴交于点E,若AE:ED=1:4,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com