
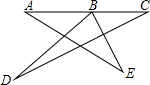
 如图所示,试求∠A+∠DBE+∠C+∠D+∠E=180°.
如图所示,试求∠A+∠DBE+∠C+∠D+∠E=180°. 分析 根据三角形外角性质和三角形内角和定理求出∠DMN=∠E+∠DBE,∠DNM=∠A+∠C,∠D+∠DMN+∠DNM=180°,即可求出∠D+∠E+∠DBE+∠A+∠C=180°.
解答 解: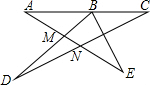
∵∠DMN=∠E+∠DBE,∠DNM=∠A+∠C,∠D+∠DMN+∠DNM=180°,
∴∠D+∠E+∠DBE+∠A+∠C=180°,
即∠A+∠DBE+∠C+∠D+∠E=180°,
故答案为:180°.
点评 本题考查了三角形外角性质,三角形的内角和定理的应用,能根据定理得出∠DMN=∠E+∠DBE,∠DNM=∠A+∠C,∠D+∠DMN+∠DNM=180°是解此题的关键,注意:三角形的内角和等于180°.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
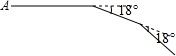 如图,小亮从A点出发前进10m,向右转18°,再前进10m,又向右转18°,…,这样一直走下去,他第一次回到出发点A时,一共走了200m.
如图,小亮从A点出发前进10m,向右转18°,再前进10m,又向右转18°,…,这样一直走下去,他第一次回到出发点A时,一共走了200m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com