
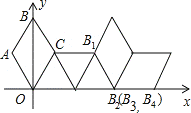
【题目】如图,在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1.将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2017次,点B的落点依次为B1,B2,B3,…,则B2017的坐标为( )
A. (1345,0) B. (1346,0) C. (1345.5,![]() ) D. (1346.5,
) D. (1346.5,![]() )
)
【答案】C
【解析】分析:
如下图,连接AC,由已知易证△ABC是等边三角形,由此可得AC=AB=OA=1,OE=![]() ,CE=
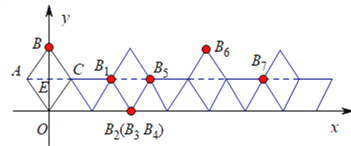
,CE=![]() ,结合图形可得B1、B2、B3、B4、B5、B6的坐标,画出后面的图形,结合图形可知每翻转6次,图形向由平移4个单位,由2017÷6=336……1,可知:点B2017相当于将点B1向右平移了336×4+1.5个单位长度得到的,由此即可得到点B2017的坐标.
,结合图形可得B1、B2、B3、B4、B5、B6的坐标,画出后面的图形,结合图形可知每翻转6次,图形向由平移4个单位,由2017÷6=336……1,可知:点B2017相当于将点B1向右平移了336×4+1.5个单位长度得到的,由此即可得到点B2017的坐标.
详解:
如下图,连接AC交OB于点E,
四边形OABC是菱形,∠ABC=60°,点B在y轴上,OA=1,
∴OA=AB=BC=OC=1,∠ABC=60°,
∴△OAC是等边三角形,∠COE=30°,
∴AC=OA=1,OE=![]() ,CE=
,CE=![]() ,
,
∴由图可知:B1、B2、B3、B4、B5、B6的坐标分别为:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 和
和![]() ;
;
∵由图可知:图形可知每翻转6次,图形向由平移4个单位,而2017÷6=336……1,
∴点B2017相当于将点B1向右平移了336×4+1.5个单位长度得到的,
∴点B2017的坐标为![]() .
.
故选C.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
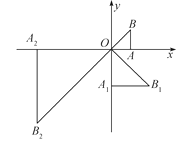
【题目】如图,在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2,且A2O=2A1O……依此规律,得到等腰直角三角形A2 017OB2 017.则点B2 017的坐标( )
A. (22 017,-22 017) B. (22 016,-22 016) C. (22 017,22 017) D. (22 016,22 016)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽暑假期间参加社会实践活动,从某批发市场以批发价每个![]() 元的价格购进
元的价格购进![]() 个手机充电宝,然后每个加价
个手机充电宝,然后每个加价![]() 元到市场出售.
元到市场出售.
![]() 求售出
求售出![]() 个手机充电宝的总售价为多少元(结果用含
个手机充电宝的总售价为多少元(结果用含![]() ,
,![]() 的式子表示)?
的式子表示)?
![]() 由于开学临近,小丽在成功售出
由于开学临近,小丽在成功售出![]() 个充电宝后,决定将剩余充电宝按售价
个充电宝后,决定将剩余充电宝按售价![]() 折出售,并很快全部售完.
折出售,并很快全部售完.
①相比不采取降价销售,她将比实际销售多盈利多少元(结果用含![]() 、
、![]() 的式子表示)?
的式子表示)?
②若![]() ,小丽实际销售完这批充电宝的利润率为________(利润率
,小丽实际销售完这批充电宝的利润率为________(利润率![]() 利润
利润![]() 进价
进价![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】麒麟区第七中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,CD=13m,AD=12m.

(1)求出空地ABCD的面积?
(2)若每种植1平方米草皮需要300元,问总共需投入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为 . 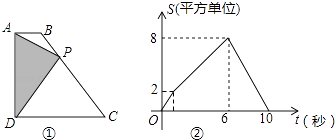
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |
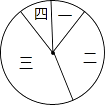
(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2 , 在第四组内的两名选手记为:B1、B2 , 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面的变形规律:
![]() ;
;![]() ;
;![]() ;….
;….
解答下面的问题:
(1)仿照上面的格式请写出![]() =_____;
=_____;
(2)若n为正整数,请你猜想![]() =_____;
=_____;
(3)基础应用:计算:![]() +
+![]() +
+![]()
![]() .
.
(4)拓展应用1:解方程:![]() +
+![]() +
+![]()
![]() =2016
=2016
(5)拓展应用2:计算:![]() +
+![]() +
+![]()
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,线段AC=6cm,线段BC=15cm,点M是AC的中点,在CB上取一点N,使得CN:NB=1:2,求MN的长.
(2)如图2,∠BOE=2∠AOE,OF平分∠AOB,∠EOF=20°.求∠AOB.
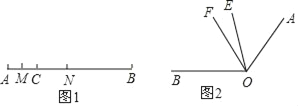
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com