
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() 和点
和点![]() .
.
(1)直接写出坐标:点![]() ,点
,点![]() .
.
(2)以线段![]() 为一边在第一象限内作正方形
为一边在第一象限内作正方形![]() .
.
则:①顶点![]() 的坐标是 ,
的坐标是 ,
②若点![]() 在双曲线
在双曲线![]() 上,试探索:将正方形
上,试探索:将正方形![]() 沿
沿![]() 轴向左平移多少个单位长度时,点
轴向左平移多少个单位长度时,点![]() 恰好落在该双曲线上.
恰好落在该双曲线上.
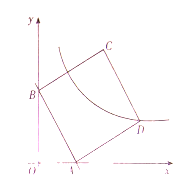
【答案】(1)![]() ;(2)①
;(2)①![]() ;②将正方形
;②将正方形![]() 沿
沿![]() 轴向左平移1个单位长度时,点
轴向左平移1个单位长度时,点![]() 恰好落在该双曲线上
恰好落在该双曲线上
【解析】
(1)利用一次函数图象上点的坐标特征可求出点A,B的坐标;
(2)①过点D作DE⊥x轴于点E,易证△OAB≌△EDA,利用全等三角形的性质可求出点D的坐标;
②由点D的坐标,利用待定系数法可求出双曲线的解析式,过点C作CF⊥y轴于点F,易证△CFB≌△AOB,利用全等三角形的性质可求出点C的坐标,再利用反比例函数图象上点的坐标特征可得出当点C落在双曲线上时正方形ABCD沿x轴向左平移的距离.
当x=0时,y=-2x+2=2,
∴点B的坐标为(0,2);
当y=0时,-2x+2=0,
解得:x=1,
∴点A的坐标为(1,0).
故答案为:(1,0);(0,2).
(2)①过点D作DE⊥x轴于点E,如图1所示.
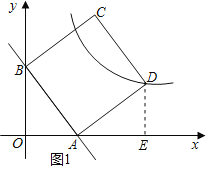
∵∠OBA+∠OAB=90°,∠OAB+∠EAD=90°,
∴∠OBA=∠EAD.
在△OAB和△EDA中,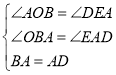 ,
,
∴△OAB≌△EDA(AAS),
∴AE=BO=2,DE=AO=1,
∴点D的坐标为(3,1).
②将点D(3,1)代入y=![]() ,得:1=
,得:1=![]() ,
,
∴k=3,
∴y=![]()
过点C作CF⊥y轴于点F,如图2所示.
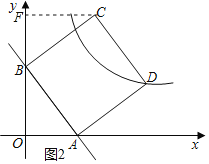
同(1)可证出△CFB≌△AOB,
∴BF=AO=1,CF=BO=2,
∴点C的坐标为(2,3).
当y=3时,![]() =3,
=3,
解得:x=1,
∵2-1=1,
∴将正方形ABCD沿x轴向左平移1个单位长度时,点C恰好落在该双曲线上.


 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC 的一边长为 10,另两边长分别是方程 x2 14 x 48 0 的两个根若用一圆形纸片将此三角形完全覆盖,则该圆形纸片的最小半径是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数的序号填在相应的横线上:
①﹣5.32,②3,③﹣1![]() ,④7%,⑤0,⑥﹣5,⑦0.6,⑧+2019
,④7%,⑤0,⑥﹣5,⑦0.6,⑧+2019
(1)整数有:_____
(2)分数有:_____
(3)负数有:_____
(4)正数有:_____
(5)非负数有:_____
(6)有理数有:_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方厘米.求截去正方形的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过一年多的精准帮扶,小明家的网络商店(简称网店)将红枣、小米等优质土特产迅速销往全国,小明家网店中红枣和小米这两种商品的相关信息如下表:
商品 | 红枣 | 小米 |
规格 | 1kg/袋 | 2kg/袋 |
成本(元/袋) | 40 | 38 |
售价(元/袋) | 60 | 54 |
根据上表提供的信息,解答下列问题:
(1)已知今年前五个月,小明家网店销售上表中规格的红枣和小米共3000kg,获得利润4.2万元,求这前五个月小明家网店销售这种规格的红枣多少袋;
(2)根据之前的销售情况,估计今年6月到10月这后五个月,小明家网店还能销售上表中规格的红枣和小米共2000kg,其中,这种规格的红枣的销售量不低于600kg.假设这后五个月,销售这种规格的红枣味x(kg),销售这种规格的红枣和小米获得的总利润为y(元),求出y与x之间的函数关系式,并求出这后五个月,小明家网店销售这种规格的红枣和小米至少获得总利润多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
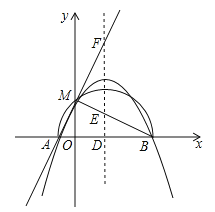
【题目】已知二次函数y=﹣x2+bx+c+1。
(1)当b=1时,求这个二次函数的对称轴的方程;
(2)若c=﹣![]() b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?
b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?
(3)若二次函数的图象与x轴交于点A(x1,0),B(x2,0),且x1<x2,b>0,与y轴的正半轴交于点M,以AB为直径的半圆恰好过点M,二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足![]() =
=![]() ,求二次函数的表达式.
,求二次函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC、BD相交于点O,点P是线段AD上一动点(不与与点D重合),PO的延长线交BC于Q点.
(1)求证:四边形PBQD为平行四边形.
(2)若AB=6cm,AD=8cm,P从点A出发.以1cm/秒的速度向点D匀速运动.设点P运动时间为t秒,问四边形PBQD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
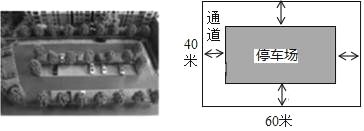
【题目】如图,城市规划部门计划在城市广场的一块长方形空地上修建乙面积为1500m2的停车场,将停车场四周余下的空地修建成同样宽的通道,已知长方形空地的长为60m,宽为40m.
(1)求通道的宽度;
(2)某公司承揽了修建停车场的工程(不考虑修通道),为了尽量减少施工对城市交通的影响,实施施工时,每天的工作效率比原计划增加了20%,结果提前2天完成任务,求该公司原计划每天修建多少m2?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com