
如图,已知△ABC,BC=5,AB=4,分别以AB、BC、CA为边向外作正方形,则图中阴影部分的面积之和的最大值是 .
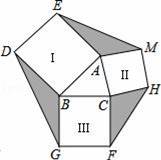

30 .
【考点】全等三角形的判定与性质;三角形的面积;正方形的性质.
【分析】把△CFH绕点C顺时针旋转90°得到△BCH′,然后判断出A、C、H′三点共线,再根据等底等高的三角形的面积相等可得S△BCH′=S△ABC,即S△CFH=S△ABC,同理可得S△BDG=S△ABC,S△AEM=S△ABC,从而得到阴影部分的面积的和=3S△ABC,再根据三角形的面积公式,当AB⊥BC时,面积最大列式计算即可得解.
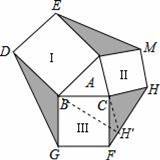
【解答】解:如图,把△CFH绕点C顺时针旋转90°得到△BCH′,
∵Ⅱ表示正方形,
∴AC=CH=CH′,∠ACH+∠BCH′=360°﹣90°×2=180°,
∴A、C、H′三点共线,
∴S△BCH′=S△ABC,
∴S△CFH=S△ABC,
同理可得S△BDG=S△ABC,S△AEM=S△ABC,
∴阴影部分的面积的和=3S△ABC,
∵BC=5,AB=4,
∴当AB⊥BC时,△ABC的面积最大,最大值为S△ABC=
 AB•AC=
AB•AC=
 ×4×5=10,
×4×5=10,
∴三个阴影部分的面积之和的最大值为3×10=30.

【点评】本题考查了正方形的性质,旋转变换的性质,利用旋转的性质作辅助线判断出每一个阴影部分的面积等于△ABC的面积是解题的关键,也是本题的难点.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
如图,直线y=2x﹣6与反比例函数y=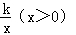 的图象交于点A(4,2),与x轴交于点B.
的图象交于点A(4,2),与x轴交于点B.
(1)求k的值及点B的坐标;
(2)在x轴上是否存在点C,使得AC=AB?若存在,求出点C的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
某地连续九天的最高气温统计如下表:
| 最高气温(℃) | 22 | 23 | 24 | 25 |
| 天数 | 1 | 2 | 2 | 4 |
则这组数据的中位数与众数分别是( )
A.24,25 B.24.5,25 C.25,24 D.23.5,24
查看答案和解析>>
科目:初中数学 来源: 题型:
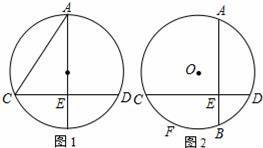
已知⊙O中弦AB⊥弦CD于E,tan∠ACD=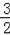

(1)如图1,若AB为⊙O的直径,BE=8,求AC的长
(2)如图2,若AB不为⊙O的直径,BE=4,F为弧BC上一点,弧BF=弧BD,且CF=7,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
2007年中国月球探测工程的“嫦娥一号”发射升空飞向月球,已知地球距离月球表面约为384000千米,那么这个距离用科学记数法表示应为( )
A、3.84×104千米 B、3.84×105千米
C、3.84×106千米 D、38.4×104千米
查看答案和解析>>
科目:初中数学 来源: 题型:
货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x千米/小时,依题意列方程正确的是( )
A.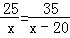 B.
B. C.
C.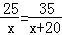 D.
D.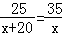
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com