Question

如图，直线y=2x﹣6与反比例函数y=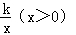的图象交于点A（4，2），与x轴交于点B．

（1）求k的值及点B的坐标；

（2）在x轴上是否存在点C，使得AC=AB？若存在，求出点C的坐标；若不存在，请说明理由．

Answer 1

【考点】反比例函数综合题．

【专题】数形结合．

【分析】（1）先把（4，2）代入反比例函数解析式，易求k，再把y=0代入一次函数解析式可求B点坐标；

（2）假设存在，然后设C点坐标是（a，0），然后利用两点之间的公式可得=，借此无理方程，易得a=3或a=5，其中a=3和B点重合，舍去，故C点坐标可求．

【解答】解：（1）把（4，2）代入反比例函数y=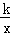，得

k=8，

把y=0代入y=2x﹣6中，可得

x=3，

故k=8；B点坐标是（3，0）；

（2）假设存在，设C点坐标是（a，0），

∵AB=AC，

∴=，

即（4﹣a）²+4=5，

解得a=5或a=3（此点与B重合，舍去）

故点C的坐标是（5，0）．

【点评】本题考查了反比函数的知识，解题的关键是理解点与函数的关系，并能灵活使用两点之间的距离公式．