

分析 (1)令y=0,求得关于x的方程x2-2x-3=0的解即为点A、B的横坐标;
(2)设P(x,x2-2x-3),根据抛物线解析式求得点D的坐标为D(1,-4);结合坐标与图形的性质求得线段CD=$\sqrt{2}$,CB=3$\sqrt{2}$,BD=2$\sqrt{5}$;所以根据勾股定理的逆定理推知∠BCD=90°,则易推知相似三角形△BCD∽△PNB,由该相似三角形的对应边成比例来求x的值,易得点P的坐标;
(3)正确做出等边△OBM和线段ME所对应的旋转线段MF,如图2.过点B,F作直线交对称轴于点G.构建全等三角形:△EOM≌△FBM,由该全等三角形的性质和图形中相关角间的和差关系得到:
∠OBF=120°为定值,即BF所在直线为定直线.过D点作DK⊥BF,K为垂足线段DF的长的最小值即为DK的长度.
解答 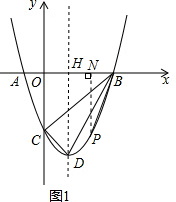 解:(1)令y=0,得x2-2x-3=0,
解:(1)令y=0,得x2-2x-3=0,
解得x1=-1,x2=3,
∴A(-1,0),B(3,0)
(2)设P(x,x2-2x-3),
如图1,过点P作PN⊥x轴,垂足为N.
连接BP,设∠NBP=∠CDB.
令x=0,得y=x2-2x-3=-3,
∴C(0,-3)
∵y=x2-2x-3=(x-1)2-4,
∴D(1,-4).
由勾股定理,得CD=$\sqrt{2}$,CB=3$\sqrt{2}$,BD=2$\sqrt{5}$.
∴BD2=BC2+CD2,
∴∠BCD=90°.
∵∠BCD=∠PNB=90°,∠NBP=∠CDB.
∴△BCD∽△PNB.
∴$\frac{PN}{BC}$=$\frac{NB}{CD}$,
$\frac{-{x}^{2}+2x+3}{3\sqrt{2}}$=$\frac{3-x}{\sqrt{2}}$,即x2-5x+6=0,
解得x1=2,x2=3(不合题意,舍去).
∴当x=2时,y=-3
∴P(2,-3);
(3)正确做出等边△OBM和线段ME所对应的旋转线段MF,如图2.
过点B,F作直线交对称轴于点G.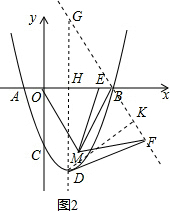
由题意可得:
$\left\{\begin{array}{l}{OM=BM}\\{ME=MF}\\{∠OME=∠BMF}\end{array}\right.$,
∴△EOM≌△FBM,
∴∠MBF=∠MOB=60°.
∵∠OBF=∠OBM+∠MBF=60°+60°=120°为定值,
∴BF所在直线为定直线.
过D点作DK⊥BF,K为垂足.
在Rt△BGH中,∠HBG=180°-120°=60°,
∴∠HGB=30°.
∵HB=3,
∴BG=4,HG=2$\sqrt{3}$.
∵D(1,-4),
∴DH=4,
∴DG=2$\sqrt{3}$+4.
在Rt△DGK中,∠DGK=30°.
∴DK=$\frac{1}{2}$DG=2+$\sqrt{3}$.
∵当点E与点H重合时,这时BF=OH=1,
则GF=4+1=5.
而GK=$\sqrt{3}$DK=3+2$\sqrt{3}$>5,即点K在点F运动的路径上,
所以线段DF的长的最小值存在,最小值是2+$\sqrt{3}$.
点评 本题考查了二次函数综合题.需要掌握抛物线与x轴的交点坐标,坐标与图形的性质,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理以及勾股定理的逆定理等知识点,难度较大,主要考查学生数形结合的数学思想方法.


科目:初中数学 来源: 题型:解答题
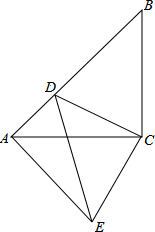 如图所示,在△ACB中,∠ACB=90°,CA=CB,D为AB边上一点,连结CD,CD绕点C逆时针旋转90度与线段CE重合,连结AE.
如图所示,在△ACB中,∠ACB=90°,CA=CB,D为AB边上一点,连结CD,CD绕点C逆时针旋转90度与线段CE重合,连结AE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7.2×10-5 | B. | -7.2×105 | C. | 7.2×106 | D. | -7.2×10-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
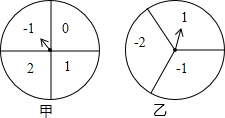 如图,甲、乙分别是4等分、3等分的两个圆转盘,指针固定,转盘转动停止后,指针指向某一数字.
如图,甲、乙分别是4等分、3等分的两个圆转盘,指针固定,转盘转动停止后,指针指向某一数字.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com