
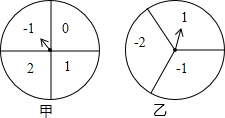
 如图,甲、乙分别是4等分、3等分的两个圆转盘,指针固定,转盘转动停止后,指针指向某一数字.
如图,甲、乙分别是4等分、3等分的两个圆转盘,指针固定,转盘转动停止后,指针指向某一数字.分析 (1)由题意可知转盘中共有四个数,其中“1”只有一种,进而求出其概率;
(2)首先根据题意列出表格,然后由表格即可求得所有等可能的结果与小华、小明获胜的情况,继而求得小华、小明获胜的概率,比较概率大小,即可知这个游戏是否公平.
解答 解:(1)甲盘停止后指针指向数字“1”的概率=$\frac{1}{4}$;
(2)列表得:
转盘A 两个数字之积 转盘B | -1 | 0 | 2 | 1 |
| 1 | -1 | 0 | 2 | 1 |
| -2 | 2 | 0 | -4 | -2 |
| -1 | 1 | 0 | -2 | -1 |
点评 本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 直线x=-$\frac{1}{3}$ | B. | 直线x=-5 | C. | 直线x=3 | D. | 直线x=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某小区有两段长度相等的道路需硬化,现分别由甲、乙两个工程队同时开始施工,如图的线段和折线是两对前6天硬化的道路长y甲、y乙(米)与施工时间x(天)之间的函数图象.
某小区有两段长度相等的道路需硬化,现分别由甲、乙两个工程队同时开始施工,如图的线段和折线是两对前6天硬化的道路长y甲、y乙(米)与施工时间x(天)之间的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com