
 ijС�������γ�����ȵĵ�·��Ӳ�����ֱַ��ɼס����������̶�ͬʱ��ʼʩ������ͼ���߶κ�����������ǰ6��Ӳ���ĵ�·��y����y�����ף���ʩ��ʱ��x���죩֮��ĺ���ͼ��
ijС�������γ�����ȵĵ�·��Ӳ�����ֱַ��ɼס����������̶�ͬʱ��ʼʩ������ͼ���߶κ�����������ǰ6��Ӳ���ĵ�·��y����y�����ף���ʩ��ʱ��x���죩֮��ĺ���ͼ������ ��1����ͼ����֪���㣬�ɸ��ݴ���ϵ�����з��̣�������ϵʽ��
��2�����÷����������M�����꣬���Խ��������⣮
��3�����Ǹ��������⣬��������ҵĹ���Ч�ʣ��з��̽����
��� �⣺��1����Y��=KX���㣨6��600������õ���K=100����Y��=100X��
0��X��2ʱ����Y��=K��X���㣨2��300������õ���K��=150����Y��=150X��
2��X��6ʱ����Y��=K��X+b��������ã�$\left\{\begin{array}{l}{2K��+b=300}\\{6K��+b=500}\end{array}\right.��\left\{\begin{array}{l}{K��=50}\\{b=200}\end{array}\right.$����Y��=50X+200��
��2���ɣ�$\left\{\begin{array}{l}{Y=100X}\\{Y=50X+200}\end{array}\right.$�õ���$\left\{\begin{array}{l}{X=4}\\{Y=400}\end{array}\right.$��
�ʵ�M��4��400������ʾ��ʵ�����壺��������4�죬�������400�ף�
��3���������ӻ���ҪX��������������⣺
500+120X=600+100X��
���X=5��
�ʻ���Ҫ5���������
���� ������Ҫ�����ô���ϵ������һ�κ�����ϵʽ��������һ�κ������ʵ�����⣮��Ҫ�߱����ù���������ʱ�������������


 ���ʿ��ÿ��ֳɳ�ϵ�д�
���ʿ��ÿ��ֳɳ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y1��y2 | B�� | y1��y2 | C�� | y1=y2 | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -5 | B�� | 4 | C�� | -3 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
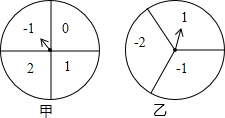 ��ͼ���ס��ҷֱ���4�ȷ֡�3�ȷֵ�����Բת�̣�ָ��̶���ת��ת��ֹͣ��ָ��ָ��ijһ���֣�
��ͼ���ס��ҷֱ���4�ȷ֡�3�ȷֵ�����Բת�̣�ָ��̶���ת��ת��ֹͣ��ָ��ָ��ijһ���֣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����D�ǡ�AOB��һ�㣬��E��OD��һ�㣬DM��OA��M��DN��OB��N��EP��OA��P��EQ��OB��Q��DM=DN����֤��EP=EQ��
��ͼ����D�ǡ�AOB��һ�㣬��E��OD��һ�㣬DM��OA��M��DN��OB��N��EP��OA��P��EQ��OB��Q��DM=DN����֤��EP=EQ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com