
【题目】如图,一次函数y=ax+b(a≠0)的图象与反比例函数y= ![]() (k≠0)的图象交于A(﹣3,2),B(2,n).
(k≠0)的图象交于A(﹣3,2),B(2,n). 
(1)求反比例函数y= ![]() 的解析式;
的解析式;
(2)求一次函数y=ax+b的解析式;
(3)观察图象,直接写出不等式ax+b< ![]() 的解集.
的解集.
【答案】
(1)解:把A(﹣3,2)代入反比例解析式得:k=﹣6,
则反比例解析式为y=﹣ ![]() ;
;
(2)解:把B(2,n)代入反比例解析式得:n=﹣3,即B(2,﹣3),
把A(﹣3,2)与B(2,﹣3)代入y=ax+b中得: ![]() ,
,
解得:a=﹣1,b=﹣1,
则一次函数解析式为y=﹣x﹣1
(3)解:∵A(﹣3,2),B(2,﹣3),
∴结合图象得:不等式ax+b< ![]() 的解集为﹣3<x<0或x>2
的解集为﹣3<x<0或x>2
【解析】(1)把A坐标代入反比例解析式求出k的值,确定出反比例解析式;(2)把B坐标代入反比例解析式求出n的值,确定出B坐标,将A与B坐标代入一次函数解析式求出a与b的值,即可确定出一次函数解析式;(3)根据A与B横坐标,结合图象确定出所求不等式的解集即可.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙P与x轴相切,与y轴相交于A(0,2),B(0,8),则圆心P的坐标是( ) 
A.(5,3)
B.(5,4)
C.(3,5)
D.(4,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解题: 学习了二次根式后,你会发现一些含有根号的式子可以写成另一个式子的平方,如3+2 ![]() =(1+
=(1+![]() )2, 我们来进行以下的探索:
)2, 我们来进行以下的探索:
设a+b![]() =(m+n
=(m+n![]() )2(其中a,b,m,n都是正整数),则有a+b
)2(其中a,b,m,n都是正整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() ,∴a=m+2n2 , b=2mn, 这样就得出了把类似a+b
,∴a=m+2n2 , b=2mn, 这样就得出了把类似a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请仿照上述方法探索并解决下列问题:
(1)当a,b,m,n都为正整数时,若a﹣b![]() =(m﹣n
=(m﹣n![]() )2 , 用含m,n的式子分别表示a,b,得a=________,b=________;
)2 , 用含m,n的式子分别表示a,b,得a=________,b=________;
(2)利用上述方法,找一组正整数a,b,m,n填空:___﹣_____![]() =(____﹣_____
=(____﹣_____![]() )2
)2
(3)a﹣4![]() =(m﹣n
=(m﹣n![]() )2且a,m,n都为正整数,求a的值.
)2且a,m,n都为正整数,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
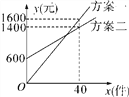
【题目】某销售公司推销一种产品,设x(件)是推销产品的数量,y(元)是付给推销员的月报酬.公司付给推销员的月报酬的两种方案如图所示,推销员可以任选一种与公司签订合同,看图解答下列问题:
(1)求每种付酬方案y关于x的函数表达式;
(2)当选择方案一所得报酬高于选择方案二所得报酬时,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在直角坐标系中,
(1)请写出△ABC各点的坐标。
(2)求出S△ABC
 (3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置,并写出A′、B′、C′的坐标。
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A′B′C′,在图中画出△ABC变化位置,并写出A′、B′、C′的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】谷歌人工智能AlphaGo机器人与李世石的围棋挑战赛引起人们的广泛关注,人工智能完胜李世石.某教学网站开设了有关人工智能的课程并策划了A,B两种网上学习的月收费方式:
收费 方式 | 月使用费(元) | 包时上网 时间(h) | 超时费(元/min) |
A | 7 | 25 | 0.6 |
B | 10 | 50 | 0.8 |
设小明每月上网学习人工智能课程的时间为x小时,方案A,B的收费金额分别为yA元,yB元.
(1)当x≥50时,分别求出yA,yB与x之间的函数关系式;
(2)若小明3月份上该网站学习的时间为60小时,则他选择哪种方式上网学习合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com