
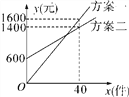
【题目】某销售公司推销一种产品,设x(件)是推销产品的数量,y(元)是付给推销员的月报酬.公司付给推销员的月报酬的两种方案如图所示,推销员可以任选一种与公司签订合同,看图解答下列问题:
(1)求每种付酬方案y关于x的函数表达式;
(2)当选择方案一所得报酬高于选择方案二所得报酬时,求x的取值范围.
【答案】(1 y=40x;y=20x+600;(2)方案一所得报酬高于方案二.
【解析】试题分析:(1)由图,已知两点,可根据待定系数法列方程,求出函数关系式;
(2)列出方程得出两直线的相交点的坐标,即可选择方案一所得报酬高于选择方案二所得报酬时x的取值范围.
试题解析:(1)设方案一的解析式为y=kx,把(40,1600)代入解析式,可得k=40,
故解析式为y=40x;
设方案二的解析式为y=ax+b,把(40,1400)和(0,600)代入解析式,
可得a=20,b=600,
故解析式为y=20x+600;
(2)根据两直线相交可得方程40x=20x+600,解得x=30.
根据两函数图象可知,当x>30时,选择方案一所得报酬高于选择方案二所得报酬.


科目:初中数学 来源: 题型:
【题目】若将点A(1,3)向左平移2个单位长度,再向下平移4个单位长度得到点B,则点B的坐标为( )
A.(-2,-1)B.(-1,0)C.(-1,-1)D.(-2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b(a≠0)的图象与反比例函数y= ![]() (k≠0)的图象交于A(﹣3,2),B(2,n).
(k≠0)的图象交于A(﹣3,2),B(2,n). 
(1)求反比例函数y= ![]() 的解析式;
的解析式;
(2)求一次函数y=ax+b的解析式;
(3)观察图象,直接写出不等式ax+b< ![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,以BC为直径作⊙O,交AC于D,E为 ![]() 的中点,连接CE,BE,BE交AC于F.
的中点,连接CE,BE,BE交AC于F. 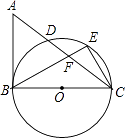
(1)求证:AB=AF;
(2)若AB=3,BC=4,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)(x3)2.(﹣x4)3 (2)(![]() x5y4﹣
x5y4﹣![]() x4y3)
x4y3)![]() x3y3
x3y3
(3)2mn.[(2mn)2﹣3n(mn+m2n)] (4)(2a+1)2﹣(2a+1)(2a﹣1)
(5)102+![]() ×(π﹣3.14)0﹣|﹣302|
×(π﹣3.14)0﹣|﹣302|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1,将Rt△ABC绕点A逆时针旋转30°后得到△AB′C′,则图中阴影部分的面积是 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com