
【题目】如图,在△ABC中,∠ABC=90°,以BC为直径作⊙O,交AC于D,E为 ![]() 的中点,连接CE,BE,BE交AC于F.
的中点,连接CE,BE,BE交AC于F. 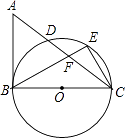
(1)求证:AB=AF;
(2)若AB=3,BC=4,求CE的长.
【答案】
(1)证明:∵E为 ![]() 的中点,
的中点,
∴ ![]() ,
,
∴∠DCE=∠CBE,
∵BC为⊙O的直径,
∴∠CEF=90°,
∴∠AFB=∠EFC=90°﹣∠DCE,
又∵∠ABF=∠ABC﹣∠CBE=90°﹣∠CBE,
∴∠ABF=∠AFB,
∴AB=AF;
(2)解:连接BD,如图所示:

∵BC为⊙O的直径,
∴∠BDC=90°,即BD⊥AC,
∵∠ABC=90°,
∴AC= ![]() =
= ![]() =5,
=5,
∵∠ADB=90°=∠ABC,∠A=∠A,
∴△ABD∽△ACB,
∴ ![]() =
= ![]() ,即
,即 ![]() ,
,
解得:AD= ![]() ,BD=
,BD= ![]() ,
,
∵AF=AB=3,
∴CF=AC﹣AF=2,DF=AF﹣AD=3﹣ ![]() =
= ![]() ,
,
∴BF= ![]() =
= ![]() ,
,
∵∠BDF=∠CEF,∠DFB=∠EFC,
∴△BDF∽△CEF,
∴ ![]() ,即
,即 ![]() ,
,
解得:CE= ![]() .
.
【解析】(1)由已知条件得出 ![]() ,由圆周角定理得出∠DCE=∠CBE,∠CEF=90°,得出∠AFB=∠EFC=90°﹣∠DCE,证出∠ABF=∠AFB,即可得出结论;(2)连接BD,由勾股定理求出AC=5,证明△ABD∽△ACB,得出对应边成比例求出AD=
,由圆周角定理得出∠DCE=∠CBE,∠CEF=90°,得出∠AFB=∠EFC=90°﹣∠DCE,证出∠ABF=∠AFB,即可得出结论;(2)连接BD,由勾股定理求出AC=5,证明△ABD∽△ACB,得出对应边成比例求出AD= ![]() ,BD=
,BD= ![]() ,由AF=AB=3,得出CF=AC﹣AF=2,DF=AF﹣AD=
,由AF=AB=3,得出CF=AC﹣AF=2,DF=AF﹣AD= ![]() ,由勾股定理求出BF,再证明△BDF∽△CEF,得出对应边成比例,即可得出结果.
,由勾股定理求出BF,再证明△BDF∽△CEF,得出对应边成比例,即可得出结果.
【考点精析】通过灵活运用圆周角定理和相似三角形的判定与性质,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE= 度;
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙P与x轴相切,与y轴相交于A(0,2),B(0,8),则圆心P的坐标是( ) 
A.(5,3)
B.(5,4)
C.(3,5)
D.(4,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生在学习《数据的分析》后,进行了检测,现将该校八(1)班学生的成绩统计如下表,并绘制成条形统计图(不完整). 
分数(分) | 人数(人) |
68 | 4 |
78 | 7 |
80 | 3 |
88 | 5 |
90 | 10 |
96 | 6 |
100 | 5 |
(1)补全条形统计图;
(2)该班学生成绩的平均数为86.85分,写出该班学生成绩的中位数和众数;
(3)该校八年级共有学生500名,估计有多少学生的成绩在96分以上(含96分)?
(4)小明的成绩为88分,他的成绩如何,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
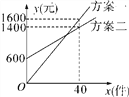
【题目】某销售公司推销一种产品,设x(件)是推销产品的数量,y(元)是付给推销员的月报酬.公司付给推销员的月报酬的两种方案如图所示,推销员可以任选一种与公司签订合同,看图解答下列问题:
(1)求每种付酬方案y关于x的函数表达式;
(2)当选择方案一所得报酬高于选择方案二所得报酬时,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:“两边及其中一边的对角分别相等的两个三角形不一定全等”.但是,小亮发现:当这两个三角形都是锐角三角形时,它们会全等,除小亮的发现之外,当这两个三角形都是 时,它们也会全等;当这两个三角形其中一个三角形是锐角三角形,另一个是 时,它们一定不全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣4,0)两点,
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)设此抛物线与直线y=﹣x在第二象限交于点D,平行于y轴的直线 ![]() 与抛物线交于点M,与直线y=﹣x交于点N,连接BM、CM、NC、NB,是否存在m的值,使四边形BNCM的面积S最大?若存在,请求出m的值,若不存在,请说明理由.
与抛物线交于点M,与直线y=﹣x交于点N,连接BM、CM、NC、NB,是否存在m的值,使四边形BNCM的面积S最大?若存在,请求出m的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com