
【题目】如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.

 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:
①∠BOE=70°; ②OF平分∠BOD;③∠POE=∠BOF; ④∠POB=2∠DOF.
其中正确的结论有_______________(填结论前面的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,以BC为直径作⊙O,交AC于D,E为 ![]() 的中点,连接CE,BE,BE交AC于F.
的中点,连接CE,BE,BE交AC于F. 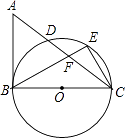
(1)求证:AB=AF;
(2)若AB=3,BC=4,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,AC平分∠DAB,∠DCA=∠DAC,试说明AB与CD的位置关系,并予以说明。

(2)如图,在(1)的结论下,AB的下方两点E,F满足:BF平分∠ABE,DF平分∠CDE,若∠DFB=20°,∠CDE=70°,求∠ABE的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)(x3)2.(﹣x4)3 (2)(![]() x5y4﹣
x5y4﹣![]() x4y3)
x4y3)![]() x3y3
x3y3
(3)2mn.[(2mn)2﹣3n(mn+m2n)] (4)(2a+1)2﹣(2a+1)(2a﹣1)
(5)102+![]() ×(π﹣3.14)0﹣|﹣302|
×(π﹣3.14)0﹣|﹣302|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠l=∠2,DE⊥BC,AB⊥BC,那么∠A=∠3吗?说明理由.

解:∠A=∠3,理由如下:
∵DE⊥BC,AB⊥BC(已知)
∴∠DEB=∠ABC=90° ( )
∴∠DEB+( )=180°
∴DE∥AB ( )
∴∠1=∠A( )
∠2=∠3( )
∵∠l=∠2(已知)
∴∠A=∠3( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A,B,C都可使小灯泡发光. 
(1)任意闭合其中一个开关,则小灯泡发光的概率等于;
(2)任意闭合其中两个开关,请用画树状图或列表的方法求出小灯泡发光的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com