【题目】已知，直线
与直线
.
【1】（1）求两直线与
轴交点A，B的坐标;
【2】（2）求两直线交点C的坐标;
【3】（3）求△ABC的面积.
【答案】
【1】(1) A（0，3）,B（0，-1）
【2】(2) C(-1,1);
【3】（3）△ABC的面积=
=2
【解析】试题分析：（1）分别令各自函数表达式中的x=0，即可求出对应y值，则两直线与y轴交点A、B的坐标可求出；
（2）联立两个一次函数的解析式，解方程组即可求出两直线交点C的坐标；
（3）由（1）可求出AB的长，由（2）可知点C的横坐标绝对值即为边AB上的高，由三角形面积公式计算即可；
试题解析：
(1)对于y＝2x＋3，令x＝0，则y＝3.
∴点A的坐标为(0，3)．
对于y＝－2x－1，令x＝0，则y＝－1.
∴点B的坐标为(0，－1)．
(2)解方程组
得
∴点C的坐标为(－1，1)．
(3)△ABC的面积为
×[3－(－1)]×|－1|＝2.
科目：初中数学 来源： 题型：
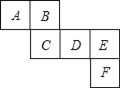
【题目】如图是一个正方体的表面展开图，请回答下列问题：
（1）与面B、C相对的面分别是 ；
（2）若A＝a3+a2b+3，B＝a2b﹣3，C＝a3﹣1，D＝﹣（a2b﹣6），且相对两个面所表示的代数式的和都相等，求E、F分别代表的代数式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了促进学生体育锻炼，某校八年级进行了体育测试，为了解女生体育测试情况，从中抽取了若干名女生的体育测试成绩.
a.体育委员小李在整理频数分布表时，不小心污染了统计表：
分组（分） | 频数 | 频数 |
21＜x≤22 | 8 | 0.200 |
22＜x≤23 | 4 | n |
23＜x≤24 | 7 | 0.175 |
24＜x≤25 | 3 | 0.075 |
25＜x≤26 | 2 | 0.050 |
26＜x≤27 | 8 | 0.200 |
27＜x≤28 | m | 0.150 |
28＜x≤29 | 2 | 0.050 |
合计 |
|
b．根据频数分布表，绘制如下频数分布直方图：
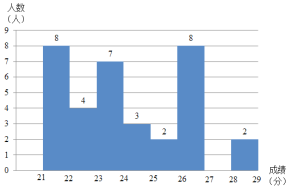
c．在此次测试中，共测试了800米，篮球，仰卧起坐，成绩统计如下：
项目 | 平均分 | 中位数 | 众数 |
800米 | 8.27 | 8.5 | 8.5 |
仰卧起坐 | 7.61 | 8 | 7.5 |
篮球 | 8.69 | 9 | 8 |
根据以上信息，回答下列问题：
（1）写出表中m，n的值；
（2）补全直方图；
（3）请结合C中统计图表，给该校女生体育训练提供建议（至少从两个不同的角度分析）.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在正方形网格中，建立如图所示的平面直角坐标系xOy，△ABC的三个顶点都在格点上，点A的坐标（4，4），请解答下列问题：
（1）画出△ABC关于y轴对称的△A1B1C1，并写出点A1、B1、C1的坐标；
（2）将△ABC绕点C逆时针旋转90°，画出旋转后的△A2B2C2，并求出点A到A2的路径长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们规定：若关于x的一元一次方程ax＝b的解为b+a，则称该方程为“和解方程”． 例如：方程2x＝﹣4的解为x＝﹣2，而﹣2＝﹣4+2，则方程2x＝﹣4为“和解方程”．
请根据上述规定解答下列问题：
（1）已知关于x的一元一次方程3x＝m是“和解方程”，求m的值；
（2）已知关于x的一元一次方程﹣2x＝mn+n是“和解方程”，并且它的解是x＝n，求m，n的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，C为线段AB的中点，点D在线段CB上．
（1）图中共有 条线段．
（2）图中AD=AC+CD，BC=AB﹣AC，类似地，请你再写出两个有关线段的和与差的关系式：
① ；② .
（3）若AB=8，DB=1.5，求线段CD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，射线OC在∠A0B的内部，图中共有3个角：∠AOB、∠AOC和∠BOC，若其中有一个角的度数是另一个角度数的两倍，则称射线OC是∠AOB的“定分线”
（1）一个角的平分线______这个角的“定分线”；（填“是”或“不是”）
（2）如图2，若∠MPN=
,且射线PQ是∠MPN的“定分线”，则∠MPQ=_____(用含a的代数式表示出所有可能的结果)
（3）如图2，若∠MPN=45°，且射线PQ绕点P从PN位置开始，以每秒10°的速度逆时针旋转，当PQ与PN成90°时停止旋转，旋转的时间为t秒.同时射线PM绕点P以每秒5°的速度逆时针旋转，并与PQ同时停止.当PQ是∠MPN的“定分线”时，求t的值。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，CD⊥AB，EF⊥AB，垂足分别为D、F，∠1＝∠2，
(1)试判断DG与BC的位置关系，并说明理由．
(2)若∠A＝70°，∠B＝40°，求∠AGD的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读以下证明过程：
已知：在△ABC中，∠C≠90°，设AB=c，AC=b，BC=a．求证：a2+b2≠c2．
证明：假设a2+b2=c2，则由勾股定理逆定理可知∠C=90°，这与已知中的∠C≠90°矛盾，故假设不成立，所以a2+b2≠c2．
请用类似的方法证明以下问题：
已知：关于x的一元二次方程x2﹣（m+1）x+2m-3=0 有两个实根x1和x2．
求证：x1≠x2．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
