
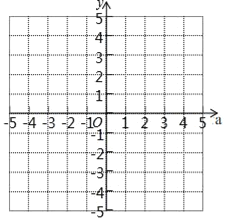
【题目】在正方形网格中,建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标(4,4),请解答下列问题:
(1)画出△ABC关于y轴对称的△A1B1C1,并写出点A1、B1、C1的坐标;
(2)将△ABC绕点C逆时针旋转90°,画出旋转后的△A2B2C2,并求出点A到A2的路径长.

科目:初中数学 来源: 题型:
【题目】已知:关于x的一元二次方程ax2﹣2(a﹣1)x+a﹣2=0(a>0).
(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为x1,x2(其中x1>x2).若y是关于a的函数,且y=ax2x1,求这个函数的表达式;
(3)将(2)中所得的函数的图象在直线a=2的左侧部分沿直线a=2翻折,图象的其余部分保持不变,得到一个新的图象.请你结合这个新的图象直接写出:当关于a的函数y=2a+b的图象与此图象有两个公共点时,b的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
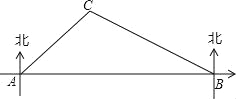
【题目】如图,在昆明市轨道交通的修建中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现测得古树C在点A的北偏东45°方向上,在点B的北偏西60°方向上,BC=400m,请你求出这段地铁AB的长度.(结果精确到1m,参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有5张写着不同数字的卡片,请按要求完成下列问题:
![]()
![]() 若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
![]() 若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
![]() 若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有3个黑球和若干白球,它们除颜色外都相同.在不允许将球倒出来数的前提下,小明为估计其中白球数,采用如下办法:随机从中摸出一球,记下颜色后放回袋中,充分摇匀后,再随机摸出一球,记下颜色,…不断重复上述过程.小明共摸100次,其中20次摸到黑球.根据上述数据,小明估计口袋中白球大约有( )
A. 10个 B. 12 个 C. 15 个 D. 18个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )

A. OE=![]() DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级所有女生的身高统计数据如下表,请回答下列问题:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) 这个学校八年级共有多少女生?
(2) 身高在 ![]() 到
到 ![]() 的女生有多少人?
的女生有多少人?
(3) 一女生的身高恰好为 ![]() ,哪一组包含这个身高?这一组出现的频数、频率各是多少?
,哪一组包含这个身高?这一组出现的频数、频率各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙0经过点D,E是⊙O上一点,且∠AED=45°,

(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为3,AE=5,求∠DAE的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD⊥DF,EC⊥DF,∠1=∠3,∠2=∠4,求证:AE∥DF.(请在下面的解答过程的空格内填空或在括号内填写理由)
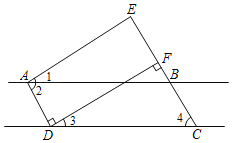
证明:∵AD⊥DF,EC⊥DF,(已知)
∴∠BFD=∠ADF=90°.( )
∴EC∥( )
∴∠EBA=_____(两直线平行,内错角相等)
∵∠2=∠4,(已知)
∴∠EBA=∠4.(等量代换)
∴AB∥_____.( )
∴∠2+∠ADC=180°.( )
∴∠2+∠ADF+∠3=180°.
∵∠1=∠3.(已知)
∴∠2+∠ADF+∠1=180°.(等量代换)
∴_____+∠ADF=180°.
∴AE∥DF.( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com