
����Ŀ����ͼ����֪AD��DF��EC��DF����1����3����2����4����֤��AE��DF������������Ľ����̵Ŀո�����ջ�����������д���ɣ�
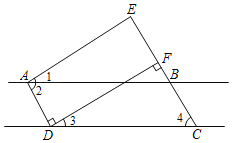
֤������AD��DF��EC��DF������֪��
���BFD����ADF��90������ ��
��EC�� ��
���EBA��_____����ֱ��ƽ�У��ڴ�����ȣ�
�ߡ�2����4������֪��
���EBA����4��������������
��AB��_____���� ��
���2+��ADC��180������ ��
���2+��ADF+��3��180����
�ߡ�1����3������֪��
���2+��ADF+��1��180����������������
��_____+��ADF��180����
��AE��DF���� ��
���𰸡�������.
��������
�����ڴ��������ֱ��ƽ�У��õ�EC��AD��������ֱ��ƽ�У��ڴ�����ȣ��ó���EBA����2�����������õ���EBA����4������ͬλ�������ֱ��ƽ�У��õ�AB��CD��������ֱ��ƽ�У�ͬ���ڽǻ����õ���2+��ADC��180�������������õ���EAD+��ADF��180�����ٸ���ͬ���ڽǻ�������ֱ��ƽ�еõ�AE��DF��
֤��������AD��DF��EC��DF������֪��
���BFD����ADF��90������ֱ�Ķ��壩��
��EC��AD���ڴ�����ȣ���ֱ��ƽ�У���
���EBA����2����ֱ��ƽ�У��ڴ�����ȣ�
�ߡ�2����4������֪��
���EBA����4��������������
��AB��DC��ͬλ����ȣ���ֱ��ƽ�У���
���2+��ADC��180������ֱ��ƽ�У�ͬ���ڽǻ�������
���2+��ADF+��3��180����
�ߡ�1����3����֪����
���2+��ADF+��1��180����������������
���EAD+��ADF��180����
��AE��DF��ͬ���ڽǻ�������ֱ��ƽ�У���
�ʴ�Ϊ����ֱ�Ķ��壬AD����2��CD��ͬλ����ȣ���ֱ��ƽ�У���ֱ��ƽ�У�ͬ���ڽǻ�������EAD��ͬ���ڽǻ�������ֱ��ƽ�У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������У�������ͼ��ʾ��ƽ��ֱ������ϵxOy����ABC���������㶼�ڸ���ϣ���A�����꣨4��4���������������⣺
��1��������ABC����y��ԳƵġ�A1B1C1����д����A1��B1��C1�����ꣻ
��2������ABC�Ƶ�C��ʱ����ת90����������ת��ġ�A2B2C2���������A��A2��·������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
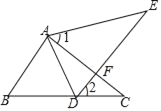
����Ŀ����ͼ����E�ڡ�ABC���ⲿ����D��BC�ϣ�DE��AC�ڵ�F������1=��2��AE=AC��BC=DE��
��1����֤��AB=AD��
��2������1=60�����жϡ�ABD����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ����ABΪһ����������ABCD��ʹP��D��������ֱ��AB�����࣮����APB=45��ʱ��PD�ij���( )��
����ABΪһ����������ABCD��ʹP��D��������ֱ��AB�����࣮����APB=45��ʱ��PD�ij���( )��

A. ![]() B.
B. ![]() C.
C. ![]() D. 5
D. 5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
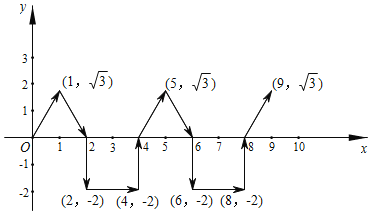
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�������ϰ����趨�����ԭ��O��������ͼ�м�ͷ��ʾ�ķ����˶�����1�δ�ԭ���˶����㣨1��![]() ������2�ν����˶����㣨2��0������3�ν����˶����㣨2����2������4�ν����˶����㣨4����2������5�ν����˶����㣨4��0������6�ν����˶����㣨5��
������2�ν����˶����㣨2��0������3�ν����˶����㣨2����2������4�ν����˶����㣨4����2������5�ν����˶����㣨4��0������6�ν����˶����㣨5��![]() �������������˶����ɣ�����2019���˶����������˶�����λ�õ�������_____��
�������������˶����ɣ�����2019���˶����������˶�����λ�õ�������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B��C��D�ĸ���վ��λ����ͼ��ʾ��A��B��վ֮��ľ���AB��a��b��B��C��վ֮��ľ���BC��2a��b��B��D��վ֮��ľ���BD��![]() a��2b��1����
a��2b��1����
��1��A��C��վ֮��ľ���AC��
��2����A��C��վ֮��ľ���AC��180km����C��D��վ֮��ľ���CD��
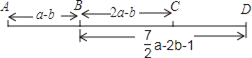
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�ŵȱ�������ֽƬ�ظ����е����4��С�����Σ���Ϊ��һ�β�����Ȼ�����е�һ�������ΰ�ͬ����ʽ�ټ���4��С�����Σ����õ�7��С�����Σ���Ϊ�ڶ��β������ٽ�����һ�������ΰ�ͬ����ʽ�ټ���4��С�����Σ����õ�10��С�����Σ���Ϊ�����β������������������ϲ�������Ҫ�õ�100��С�����Σ�����Ҫ�����Ĵ�����(����)
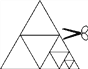
A. 25 B. 33 C. 34 D. 50
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ��չ��������Ƽ����±����������ϲ�����������������һ��ң�س���ֱ�߹��AC������ֱ���˶���ģ�ͣ��ס�������ͬʱ�ֱ��A��B�����������ع������C����B��AC�ϣ����ٶ����ҵ��ٶȵ�1��5������t���֣���ס�����ң�س���B���ľ���ֱ�Ϊd1��d2����d1��d2��t�ĺ�����ϵ��ͼ���Ը���ͼ�����������⣺
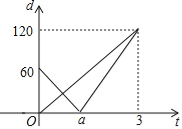
��1����գ��ҵ��ٶ�v2= ��/�֣�
��2��д��d1��t�ĺ�����ϵʽ��
��3�����ס�����ң�س��ľ��볬��10��ʱ�źŲ����������ţ���̽��ʲôʱ����ң�س����źŲ����������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
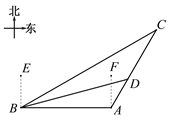
����Ŀ����ͼ��ij���ҹ�һ�Һ��ബѲ����A�ۿ���������B��ʱ��������B�ı�ƫ��60�㷽�����150���ﴦ��C����һ���ɴ�ֻ����CA������ʻ��C����A�ۿڵı�ƫ��30�㷽���ϣ����ബ��A�ۿڷ���ָ�ִ����������A�ۿ���AC����ʻ������D���ɹ����ؿ��ɴ�ֻ����ʱD����B��ľ���Ϊ75![]() ���
���
(1)��B�㵽ֱ��CA�ľ��룻
(2)ִ������A��D�����˶��ٺ����![]() ��1.414��
��1.414��![]() ��1.732�������ȷ��0.1���
��1.732�������ȷ��0.1���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com