
【题目】已知![]() ,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.当∠APB=45°时,PD的长是( );
,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.当∠APB=45°时,PD的长是( );

A. ![]() B.
B. ![]() C.
C. ![]() D. 5
D. 5
【答案】A
【解析】
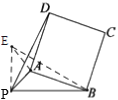
过P作PB的垂线,过A作PA的垂线,两条垂线相于与E,连接BE,由∠APB=45°可得∠EPA=45°,可得△PAE是等腰直角三角形,即可求出PE的长,根据角的和差关系可得∠EAB=∠PAD,利用SAS可证明△PAD≌△EAB,可得BE=PD,利用勾股定理求出BE的长即可得PD的长.
过P作PB的垂线,过A作PA的垂线,两条垂线相交与E,连接BE,
∵∠APB=45°,EP⊥PB,
∴∠EPA=45°,
∵EA⊥PA,
∴△PAE是等腰直角三角形,
∴PA=AE,PE=![]() PA=2,
PA=2,
∵四边形ABCD是正方形,
∴∠EAP=∠DAB=90°,
∴∠EAP+∠EAD=∠DAB+∠EAD,即∠PAD=∠EAB,
又∵AD=AB,PA=AE,
∴△PAD≌△EAB,
∴PD=BE=![]() =
=![]() =2
=2![]() ,
,
故选A.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】如图,现有5张写着不同数字的卡片,请按要求完成下列问题:
![]()
![]() 若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
若从中取出2张卡片,使这2张卡片上数字的乘积最大,则乘积的最大值是______.
![]() 若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
若从中取出2张卡片,使这2张卡片上数字相除的商最小,则商的最小值是______.
![]() 若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
若从中取出4张卡片,请运用所学的计算方法,写出两个不同的运算式,使四个数字的计算结果为24.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙0经过点D,E是⊙O上一点,且∠AED=45°,

(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为3,AE=5,求∠DAE的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代的数学专著,是“算经十书”(汉唐之间出现的十部古算书)中最重要的一种.书中有下列问題:“今有邑方不知大小,各中开门,出北门八十步有木,出西门二百四十五步见木,问邑方有几何?”意思是:如图,点![]() 、点
、点![]() 分别是正方形
分别是正方形![]() 的边
的边![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() 过点
过点![]() ,
,![]() 步,
步,![]() 步,则正方形的边长为( )
步,则正方形的边长为( )

A.![]() 步B.
步B.![]() 步C.
步C.![]() 步D.
步D.![]() 步
步
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是1个直角三角形和2个小正方形,直角三角形的三条边长分别是a,b,c,其中a,b是直角边,正方形的边长分别是a、b.
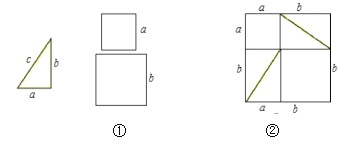
(1)将4个完全一样的直角三角形和2个小正方形构成一个大正方形(如图②).用两种不同的方法列代数式表示图②中的大正方形面积:
方法一:______________________________;
方法二:______________________________;
(2)观察图②,试写出![]() ,
,![]() ,
,![]() ,
,![]() 这四个代数式之间的等量关系;
这四个代数式之间的等量关系;
(3)利用(2)的结论计算![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是等边三角形,点D、E分别是边BC、CA上的点,且BD=CE,AD、BE相交于点O.

(1)求证:△BAE≌△ACD;
(2)求∠AOB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD⊥DF,EC⊥DF,∠1=∠3,∠2=∠4,求证:AE∥DF.(请在下面的解答过程的空格内填空或在括号内填写理由)
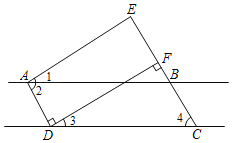
证明:∵AD⊥DF,EC⊥DF,(已知)
∴∠BFD=∠ADF=90°.( )
∴EC∥( )
∴∠EBA=_____(两直线平行,内错角相等)
∵∠2=∠4,(已知)
∴∠EBA=∠4.(等量代换)
∴AB∥_____.( )
∴∠2+∠ADC=180°.( )
∴∠2+∠ADF+∠3=180°.
∵∠1=∠3.(已知)
∴∠2+∠ADF+∠1=180°.(等量代换)
∴_____+∠ADF=180°.
∴AE∥DF.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知P(-5,m)和Q(3,m)是二次函数y=2x2+bx+1图象上的两点.
(1)求b的值;
(2)将二次函数y=2x2+bx+1的图象沿y轴向上平移k(k>0)个单位,使平移后的图象与x轴无交点,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题原型)如图,在![]() 中,对角线
中,对角线![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .求证:四边形
.求证:四边形![]() 是菱形.
是菱形.
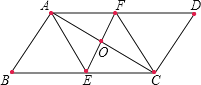
(小海的证法)证明:
![]()
![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]()
![]() ,(第一步)
,(第一步)
![]() ,(第二步)
,(第二步)
![]() .(第三步)
.(第三步)
![]() 四边形
四边形![]() 是平行四边形.(第四步)
是平行四边形.(第四步)
![]() 四边形
四边形![]() 是菱形. (第五步)
是菱形. (第五步)
(老师评析)小海利用对角线互相平分证明了四边形![]() 是平行四边形,再利用对角线互相垂直证明它是菱形,可惜有一步错了.
是平行四边形,再利用对角线互相垂直证明它是菱形,可惜有一步错了.
(挑错改错)(1)小海的证明过程在第________步上开始出现了错误.
(2)请你根据小海的证题思路写出此题的正确解答过程,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com