
【题目】(问题原型)如图,在![]() 中,对角线
中,对角线![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .求证:四边形
.求证:四边形![]() 是菱形.
是菱形.
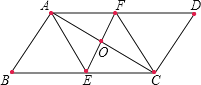
(小海的证法)证明:
![]()
![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]()
![]() ,(第一步)
,(第一步)
![]() ,(第二步)
,(第二步)
![]() .(第三步)
.(第三步)
![]() 四边形
四边形![]() 是平行四边形.(第四步)
是平行四边形.(第四步)
![]() 四边形
四边形![]() 是菱形. (第五步)
是菱形. (第五步)
(老师评析)小海利用对角线互相平分证明了四边形![]() 是平行四边形,再利用对角线互相垂直证明它是菱形,可惜有一步错了.
是平行四边形,再利用对角线互相垂直证明它是菱形,可惜有一步错了.
(挑错改错)(1)小海的证明过程在第________步上开始出现了错误.
(2)请你根据小海的证题思路写出此题的正确解答过程,
 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车同时分别从A,B两处出发,沿轨道到达C处,B在AC上,甲的速度是乙的速度的1.5倍,设t(分)后甲、乙两遥控车与B处的距离分别为d1,d2,则d1,d2与t的函数关系如图,试根据图象解决下列问题:
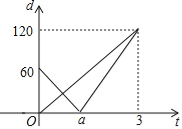
(1)填空:乙的速度v2= 米/分;
(2)写出d1与t的函数关系式:
(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探求什么时间两遥控车的信号不会产生相互干扰?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题:
(1)4+(-2)=_____________; (2)-3-(-2)=__________;
(3)-2×5=_____________; (4)-6÷(-3)=__________;
(5)![]() =_____________; (6)
=_____________; (6)![]() =__________;
=__________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形 ABCD 的边长为 8,E 是 BC 边的中点,点 P 在射线 AD 上, 过 P 作 PF⊥AE 于 F.
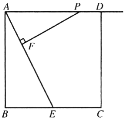
(1)请判断△PFA 与△ABE 是否相似,并说明理由;
(2)当点 P 在射线 AD 上运动时,设 PA=x,是否存在实数 x,使以 P,F,E 为顶 点的三角形也与△ABE 相似?若存在,请求出 x 的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级甲,乙两班各有![]() 名学生,为了解这两个班学生身体素质情况,进行了抽样调查.从这两个班各随机抽取
名学生,为了解这两个班学生身体素质情况,进行了抽样调查.从这两个班各随机抽取![]() 名学生进行身体素质测试,测试成绩如下:
名学生进行身体素质测试,测试成绩如下:
甲班![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
乙班![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
整理上面数据,得到如下统计表:

样本数据的平均数、众数.中位数如下表所示:
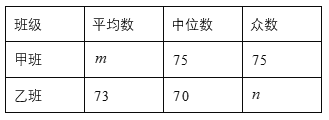
根据以上信息,解答下列问题:
(1)求表中![]() 的值
的值
(2)表中![]() 的值为( )
的值为( )
(3)若规定测试成绩在![]() 分以上(含
分以上(含![]() 分)的学生身体素质为优秀,请估计乙班
分)的学生身体素质为优秀,请估计乙班![]() 名学生中身体素质为优秀的学生的人数.
名学生中身体素质为优秀的学生的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
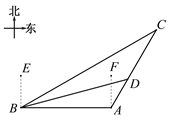
【题目】如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(![]() ≈1.414,
≈1.414,![]() ≈1.732,结果精确到0.1海里)
≈1.732,结果精确到0.1海里)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形![]() 的边
的边![]() 在数轴上,
在数轴上,![]() 为原点,长方形
为原点,长方形![]() 的面积为12,
的面积为12,![]() 边的长为3.
边的长为3.
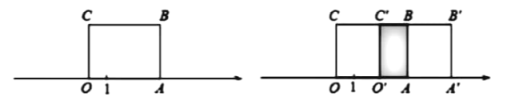
(1)数轴上点![]() 表示的数为________.
表示的数为________.
(2)将长方形![]() 沿数轴水平移动,移动后的长方形记为
沿数轴水平移动,移动后的长方形记为![]() ,设长方形
,设长方形![]() 移动的距离为
移动的距离为![]() ,移动后的长方形
,移动后的长方形![]() 与原长方形
与原长方形![]() 重叠部分的面积记为
重叠部分的面积记为![]() .
.
①当![]() 等于原长方形
等于原长方形![]() 面积的
面积的![]() 时,则点
时,则点![]() 的移动距离
的移动距离![]() _______,此时数轴上点
_______,此时数轴上点![]() 表示的数为_______.
表示的数为_______.
②![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() 当点
当点![]() ,
,![]() 所表示的数互为相反数时,则
所表示的数互为相反数时,则![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意有理数a,b,定义运算:a⊙b=a(a+b)﹣1,等式右边是通常的加法、减法、乘法运算,例如,2⊙5=2×(2+5)﹣1=13;(﹣3)⊙(﹣5)=﹣3×(﹣3﹣5)﹣1=23.
(1)求(﹣2)⊙3![]() 的值;
的值;
(2)对于任意有理数m,n,请你重新定义一种运算“⊕”,使得5⊕3=20,写出你定义的运算:m⊕n= (用含m,n的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com