
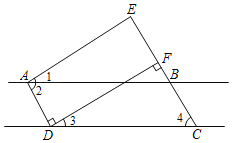
【题目】如图,点E在△ABC的外部,点D边BC上,DE交AC于点F,若∠1=∠2,AE=AC,BC=DE.
(1)求证:AB=AD;
(2)若∠1=60°,判断△ABD的形状,并说明理由.
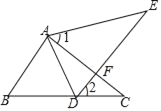
【答案】(1)见解析;(2)△ABD是等边三角形.理由见解析.
【解析】分析:
(1)由∠1=∠2结合∠AFE=∠DFC可得∠E=∠C,这样结合AE=AC,BC=DE即可证得△ABC≌△ADE,由此即可得到AB=AD;
(2)由∠1=∠2=60°可得∠BDE=120°,由△ABC≌△ADE可得∠B=∠ADE,AB=AD,进而可得∠B=∠ADB=∠ADE,由此即可得到∠ADB=![]() ∠BDE=60°,这样结合AB=AD即可得到△ABD是等边三角形.
∠BDE=60°,这样结合AB=AD即可得到△ABD是等边三角形.
详解:
(1)∵∠1+∠AFE+∠E=180°,∠2+∠CFD+∠C=180°,∠1=∠2,∠AFE=∠CFD,
∴∠E=∠C,
∵AC=AE,∠C=∠E,BC=DE,
∴△ABC≌△ADE,
∴AB=AD.
(2)△ABD是等边三角形.理由如下:
∵∠1=∠2=60°,
∴∠BDE=180°﹣∠2=120°,
∵△ABC≌△ADE,
∴∠B=∠ADE,AB=AD,
∴∠B=∠ADB,
∴∠ADB=∠ADE,
∴∠ADB=![]() ∠BDE=60°,
∠BDE=60°,
∴△ABD是等边三角形.


科目:初中数学 来源: 题型:
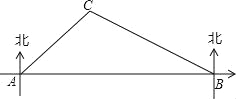
【题目】如图,在昆明市轨道交通的修建中,规划在A、B两地修建一段地铁,点B在点A的正东方向,由于A、B之间建筑物较多,无法直接测量,现测得古树C在点A的北偏东45°方向上,在点B的北偏西60°方向上,BC=400m,请你求出这段地铁AB的长度.(结果精确到1m,参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级所有女生的身高统计数据如下表,请回答下列问题:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) 这个学校八年级共有多少女生?
(2) 身高在 ![]() 到
到 ![]() 的女生有多少人?
的女生有多少人?
(3) 一女生的身高恰好为 ![]() ,哪一组包含这个身高?这一组出现的频数、频率各是多少?
,哪一组包含这个身高?这一组出现的频数、频率各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙0经过点D,E是⊙O上一点,且∠AED=45°,

(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为3,AE=5,求∠DAE的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在平面直角坐标系中直线y=x﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).
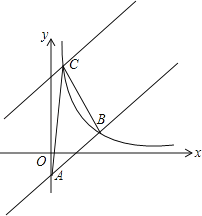
(1)求反比例函数的关系式;
(2)将直线y=x﹣2向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代的数学专著,是“算经十书”(汉唐之间出现的十部古算书)中最重要的一种.书中有下列问題:“今有邑方不知大小,各中开门,出北门八十步有木,出西门二百四十五步见木,问邑方有几何?”意思是:如图,点![]() 、点
、点![]() 分别是正方形
分别是正方形![]() 的边
的边![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() 过点
过点![]() ,
,![]() 步,
步,![]() 步,则正方形的边长为( )
步,则正方形的边长为( )

A.![]() 步B.
步B.![]() 步C.
步C.![]() 步D.
步D.![]() 步
步
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是1个直角三角形和2个小正方形,直角三角形的三条边长分别是a,b,c,其中a,b是直角边,正方形的边长分别是a、b.
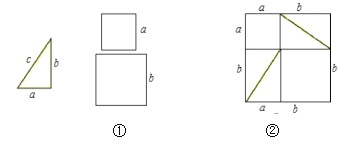
(1)将4个完全一样的直角三角形和2个小正方形构成一个大正方形(如图②).用两种不同的方法列代数式表示图②中的大正方形面积:
方法一:______________________________;
方法二:______________________________;
(2)观察图②,试写出![]() ,
,![]() ,
,![]() ,
,![]() 这四个代数式之间的等量关系;
这四个代数式之间的等量关系;
(3)利用(2)的结论计算![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD⊥DF,EC⊥DF,∠1=∠3,∠2=∠4,求证:AE∥DF.(请在下面的解答过程的空格内填空或在括号内填写理由)
证明:∵AD⊥DF,EC⊥DF,(已知)
∴∠BFD=∠ADF=90°.( )
∴EC∥( )
∴∠EBA=_____(两直线平行,内错角相等)
∵∠2=∠4,(已知)
∴∠EBA=∠4.(等量代换)
∴AB∥_____.( )
∴∠2+∠ADC=180°.( )
∴∠2+∠ADF+∠3=180°.
∵∠1=∠3.(已知)
∴∠2+∠ADF+∠1=180°.(等量代换)
∴_____+∠ADF=180°.
∴AE∥DF.( )
查看答案和解析>>
科目:初中数学 来源: 题型:
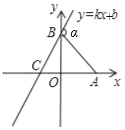
【题目】如图,已知A点坐标为(5,0),直线y=kx+b(b>0)与y轴交于点B,∠BCA=60°,连接AB,∠α=105°,则直线y=kx+b的表达式为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com