
【题目】如图所示,在△ABC中,∠ABC=45°.点D在AB上,点E在BC上,且AE⊥CD,若AE=CD,BE:CE=5:6,S△BDE=75,则S△ABC=_____.

【答案】440.
【解析】
作DM⊥BC于M,AN⊥BC于N,利用AAS证出△AEN≌△CDM,从而得出AN=CM,EN=DM,设BE=5a,用含a的式子分别表示各个线段的长度,根据三角形的面积公式即可求出a2,然后根据三角形的面积公式求面积即可.
解:作DM⊥BC于M,AN⊥BC于N,如图所示:

则∠CMD=∠BMD=∠ANE=90°,
∵∠ABC=45°,
∴△BDM、△BAN是等腰直角三角形,
∴BM=DM,BN=AN,
∵AE⊥CD,
∴∠AEN+∠EAN=∠AEN+∠DCM=90°,
∴∠EAN=∠DCM,
在△AEN和△CDM中,
 ,
,
∴△AEN≌△CDM(AAS),
∴AN=CM,EN=DM,
∴BN=CM,
∴BM=CN,
∴BM=DM=CN=EN,
∵BE:CE=5:6,
∴设BE=5a,
则CE=6a,BC=BE+CE=11a,BM=DM=CN=EN=![]() CE=3a,AN=CM=BC﹣BM=8a,
CE=3a,AN=CM=BC﹣BM=8a,
∴CD2=DM2+CM2=(3a)2+(8a)2=73a2,
∵S△BDE=![]() BE×DM=
BE×DM=![]() ×5a×3a=75,
×5a×3a=75,
∴a2=10,
∴S△ABC=![]() BC×AN=
BC×AN=![]() ×11a ×8a=44 a2=440;
×11a ×8a=44 a2=440;
故答案为:440.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
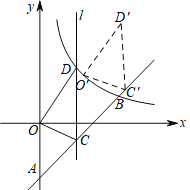
【题目】如图,一次函数y=kx-4(k≠0)的图象与y轴交于点A,与反比例函数y=![]() (x>0)的图象交于点B(6,b).
(x>0)的图象交于点B(6,b).
(1)b=__________;k=__________.
(2)点C是直线AB上的动点(与点A,B不重合),过点C且平行于y轴的直线l交这个反比例函数的图象于点D,当点C的横坐标为3时,得△OCD,现将△OCD沿射线AB方向平移一定的距离(如图),得到△O′C′D′,若点O的对应点O′落在该反比例函数图象上,求点O′,D′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解初中各年级学生每天的平均睡眠时间(单位:h,精确到1 h),抽样调查了部分学生,并用得到的数据绘制了下面两幅不完整的统计图.
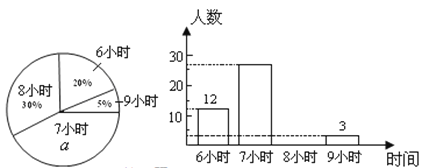
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中百分数![]() 的值为_______,所抽查的学生人数为______;
的值为_______,所抽查的学生人数为______;
(2)求出平均睡眠时间为8小时的人数,并补全条形图;
(3)求出这部分学生的平均睡眠时间的平均数;
(4)如果该校共有学生1200名,请你估计睡眠不足(少于8小时)的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
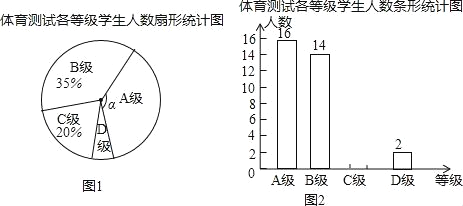
【题目】为了解某区九年级学生身体素质情况,该区从全区九年级学生中随机抽取了部分学生进行了一次体育考试科目测试(把测试结果分为四个等级:A级:优秀:B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如图两幅不完整的统计图.请根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 ;
(2)求图1中∠α的度数是 °,把图2条形统计图补充完整;
(3)该区九年级有学生3500名,如果全部参加这次体育科目测试,请估计不及格的人数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都市电力公司为了鼓励居民节约用电,采用分段计费的方法计算电费;第一档:每月用电不超过180度时,按每度0.5元计费;第二档:每月用电超过180度但不足280度时,其中超过部分按每度0.6元计费;第三档:280度以上时,超出部分按每度0.8元计费.
(1)若李明家1月份用电160度应交电费 元,2月份用电200度应交电费 元.
(2)若设用电量为x度,应交电费为y元,请求出这三档中y与x的关系式.并利用关系式求交电费108元时的用电量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,BA=BC,∠ABC=100°,AB平分∠WAC.在线段AC上有一动点D,连接BD并作∠DBE,使∠DBE=50°,BE边交直线AW于点E,连接DE.
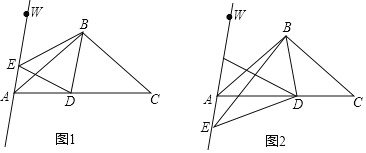
(1)如图1,当点E在射线AW上时,直接判断:AE+DE CD;(填“>”、“=”或“<”)
(2)如图2,当点E在射线AW的反向延长线上时,
①判断线段CD,DE,AE之间的数量关系,并证明;
②若S四边形ABDE﹣S△BCD=6,且2DE=5AE,AD=![]() AE,求S△ABC的值.
AE,求S△ABC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,BC=6,AB=10.点Q与点B在AC的同侧,且AQ⊥AC.

(1)如图1,点Q不与点A重合,连结CQ交AB于点P.设AQ=x,AP=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(2)是否存在点Q,使△PAQ与△ABC相似,若存在,求AQ的长;若不存在,请说明理由;
(3)如图2,过点B作BD⊥AQ,垂足为D.将以点Q为圆心,QD为半径的圆记为⊙Q.若点C到⊙Q上点的距离的最小值为8,求⊙Q的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com